We need Pi

SOD's first CAD poser caused me to wonder whether it could be drawn using virtual hexagons and while mulling that over I started wondering about PI.

Hexagons in circles we drew at school to make pretty patterns with our compasses with the simiplicity that using the Radius of the circle to mark points on the circumference effectively gives 6 equailateral triangles with every internal angle being 60deg.

Looking up how computer programs work out the extreme numbers of decimal places of PI got to formulae that are simply beyond me but also got me thinking about using the perimeter of my hexagon inscribed inside circle and outside the circle as averages.

I found this neatly simple explanation of Archimedes method in it;s elegant simplicity:

**LINK**

pgk

22/7 is often close enough for me. Mosttimes it is easier to accept the value than derive it - unless you like to be a mathematician.

A bit like working out why ‘mosttimes’ is usually two words but ‘sometimes’ is generally one word.🙂

There are infinite series representations of pi, so it would be simple, if tedious, to do the calculations. Many of the series are based on i, so that makes things a bit more complex (pun intended). Modern methods use iterative algorithms rather than grunt calculation of an infinite series, as they converge more quickly. The development of fast algorithms for multiplying large numbers also helped. An interesting problem is how do you keep track of a million plus digit number. A 32-bit, or even 64-bit binary word isn't going to cut the mustard.

The modern concepts of sine, cosine and tangent were developed in the early medieval period, mainly in Middle East and later Europe. One name missing in the OP is Euclid. He developed the first geometry based on a plane. What most people now call geometry is actually Euclidian geometry, albeit re-defined by Descartes. It wasn't until the 19th century that it was realised that many different forms of geometry can be constructed, although Euclid did do some early work on spherical geometry.

Andrew

355/113 is a bit more accurate, good enough for most workshop stuff.

Mike

"elegant simplicity"

Umm ... yes, indeed! However given the 'ad infinitum' nature of pi calculations. anything beyond 22/7 makes my head hurt and my eyeballs fall out!!

rgds

Bill

This worked all right when using a blunt pencil and a pair of school compasses with the dried blood scraped off the point. However, when I borrowed Grandpa's draughting set, I found that, no matter how I tried, I could never get the last circle to coincide with the first. It was only later that I discovered that this is because the value of pi is more than three.

It was when I was studying electrical engineering some years later that I discovered the mnemonic "How I need a drink, alcoholic of course, after the heavy chapters involving quantum mechanics" which by counting the letters gives pi to 15 sig. figs. though I never found a use for it.

Then when I learned computer programming (remember Algol on punched cards, anyone?) I learned that pi equals 4*arctan(1). Much more useful.

These days I just press a button on my calculator.

George B.

+1 for the calculator.

But I must confess that, at University, I took it upon myself the learn pi to 10 significant figures, which was the precision of the calculator that I had at the time. And I can still remember it 40 years later!

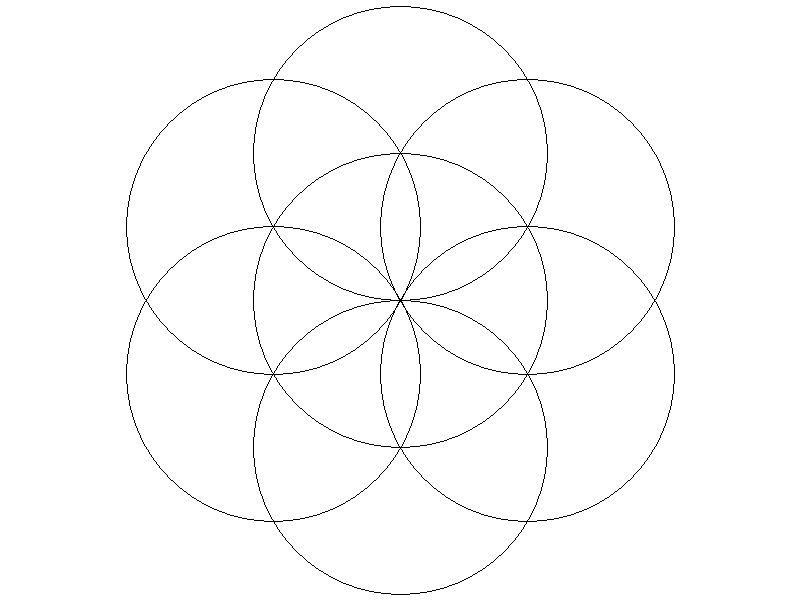
I agree that Pi on a calculator is the easy way. I also agree that often my attmepts at drawing interlocking circles failed but that is our/my failure to be neat enough and nothing to do with Pi as Turbocad can easily prove:

pgk

Maybe I'm good with numbers but I've never had any trouble remembering Pi as 3.14159 since learning it back in about 1968. 22/7 doesn't come close, and 355/113 is even harder to remember.

I can also quote from memory the registration plate number for most cars I have owned, my bank account, health care card, drivers license and several other numbers that I use with varying frequency.

I'm pretty normal otherwise......

..give it another decade

As a student with my first car - Austen A30 - I made up number plates from scrapyard letters glued to a blank plate. Recovering one morning from a boozy party during a thunderstorm I wasstopped by a policeman (back in the days of beat police who would step into the road and stick a hand up) demanding to know my reg number. Hangover and bad humour caused me to suggest he just look at the back or front of the vehicle. A bad move when it turned out the thunderstorm had dissolved whatever glue I'd used and the plates were both blank.

Fortunately police were a tad more tolerant back then and i was accompnied to buy a pot of paint and a brush.

pgk

For pi to 30 places (3.141592653589793238462643383276), here's a list of approximations, poor to good, and their error as a percentage to 3 places:

pi=3 Error 4.507%
pi=3.1 Error 1.324%
pi=3.14 Error 0.507%
pi=22/7 Error -0.040%
pi=3.141 Error 0.019%
pi=3.1415 Error = 0.003%
pi=355/133 Error = 0.000085%
pi=3.14159 Error = 0.000084%
pi=3.141592 Error = 0.000020%

pi to 30 places of decimals compared with pi to 100 places is a really tiny error, a little over: -0.0000000000000000000000000001%

For workshop tasks 22/7 is comfy for pencil and paper arithmetic and the result is plenty good enough for most practical purposes. Remembering pi ≈ 3.141 and doing the sum in decimal halves the error caused by 22/7, not that it matters much for ordinary work.

Now we have calculators, I don't rate 355/113 in practice. Multiplying by 355 and dividing by 113 with paper and pencil is hard work! Better to memorise 3.14159, which is slightly more accurate. Best of all is the value of pi stored in a calculator, which is more accurate again, and it doesn't have to be remembered at all. Why risk making mistakes with clumsy fractions?

Some reasons why pi needs to be accurate

• the object is very large, like the radius of our universe,
• a high level of accuracy is demanded, as in the Global Positioning System,
• the object is very small, like an atomic particle;
• some iterative calculations lose accuracy due to rounding errors.
• number theory, mathematical exploration and computer improvements

In practice, GPS only uses 16 digits. Atomic science seems the main application for very high accuracy but even they only use 32 digit pi in calculations.

My computer can easily do pi to a 1000 digits, but it's a novelty. In the workshop I normally use 3.141 and a calculator. At school most calculations were done with a slide-rule only roughly representing 3.14, and I don't remember it ever not being 'good enough'. I know a more accurate pi was in a book of Mathematical Tables but don't recall ever using it. (Could be because I was a lazy student and bored by maths!)

The different ways of calculating pi are fascinating and researching them opened many high-technology doors. Everything from weather forecasting to Light Emitting Diodes and the Internet.

Dave

Immaterial but we always rounded up to 3.142

pgk

Very sensible, it reduces the error to 0.013%. I may not have been paying attention on that day...

Dave

I often use 22/7 as it is easy enough to do many calcs in my head. I haver never smoked so ‘back of a fag packet’ was rarely an option.

When I was at Loughborough ... The University Library took a little periodical named Pi

Printed along the top edge [if I recall correctly] of each issue was the continuing series of numbers.

... It would be nice to think it’s still running.

MichaelG.

At school I used 3.142 and still haven’t forgotten the log was 0.4972 which I wrote at the bottom of the page in my four figure tables, I remember 3.14159 these days if I have a calculator without a pi button, both my sliderules have a pi mark on the scales but these only come out for curiosity to see if anyone under 64 knows what it is. Considering some of our great engineering feats were made without a calculator or even a computer I don’t think people realise what a powerful tool the pocket scientific calculator especially the programmable and graphing models.

Mike

The great think about Pi is that after ten digits you can make it up and no-one knows you are bluffing

Neil

P.S. Georgineer - me too. I reckon it's all made up this equilateral stuff.

Numbers are wonderful. If you take 22/7 you will get 3.142857142857142857 recurring.

If you throw away the three and the recurring bits you are left with 142857. This is a magic number! Multiply it with any digit from 1-6 you will still find this number eg 142857x 5=714285. 142857 rotated! Multiply by 7 and you get 999,999. But, it does not end there, try multiplying by a larger number and the magic number is still there!For example 142857x18 gives you 2,571,426. Where is the number? Start at the one, so 142, add the six and the two from the front, you get eight and finish with a flourish with five and seven. I love numbers!

My two favourite methods to calculate Pi are using random numbers https://www.youtube.com/watch?v=RZBhSi_PwHU  and using a balance beam **LINK**

Hopefully promotion of his book and patron page dont fall foul of the new rules.

Adrian

Edited By AdrianR on 05/07/2020 18:06:36

What,s wrong with 3 and a bit ?