Cutting parallel tooth gears
Calculation queries on setup
| Geoff Lewis 1 | 31/10/2013 11:26:05 |
| 10 forum posts 12 photos | I'm building a 1/8 scale working model of a 1940/50's era mechanical shovel and presently working on the vertical bevel gear drive to power the whole machine along forward or backwards. The horizontal bevel is has 22 teeth of 14 DP and a PCD of 1.5714 inch The verical Bevel is 24 teeth with 14 DP and a PCD of 1.7142 The teeth will be parallel cut and I have been using information gleaned from'Gears & Gear Cutting' by Ivan Law. Each gears has been set out and drawn as per the text and blanks have been machined ready for cutting teeth. Whoopee! I have a dividing plate with both 22 and 24 holes so the basic cut should not be a problem. I am a little confused with the calculations on page 106 however for establishing the amount of offset required. The illustration used is pretty straight forward using a mite gear having 90 degree cone which I assume is waht is refered to in the following calculation:-
At other points prior to this calculation he refers to SIN 45 = 0.707
and the 24 tooth gear a cone angle of 95 Degrees SINE, TANGENT and COSINE are calculations based on a right angle triangle so in one sense I cannot use it for my 24 tooth gear. HOWEVER! When I punch in SIN 85 and SIN 95 on my calculator they both give the same answer of 0.9962 On page 111 left hand column it says : The calculation is always the same and concists of simply multiplying half the pitch diameter by the sine of the angle, 90/ Number of teeth. AM I MISSING SOMETING? Any clarification of the above would be much appreciated. |
| jason udall | 31/10/2013 13:40:50 |
| 2032 forum posts 41 photos | I am no expert in gears but. Yes sin 85 does equal sin 95.. infact for 0 to 180 degree , sine is symetrical about 90 degrees so sin (90 -t) = sin ( 90+t) The same thing happens at 270 degrees for 90 degrees either side ( 180 to 360 ) |
| Stub Mandrel | 31/10/2013 14:11:42 |
4318 forum posts 291 photos 1 articles | Hi Geoff, Two essential points: 1 there is an error in Ivan's book. On P108 column 2 the calvculations for o/dia small end and o'dia big end should BOTH use COS not SIN. 2 Ivan's cone angle is HALF the included angle so, assuming your bevels are at 90 degrees the angles are 42.5 and 55.5. I have made asymmetrical bevels using Ivan's method and they worked! If you have any furher questions - just ask Neil
|
| KWIL | 31/10/2013 17:04:16 |
| 3681 forum posts 70 photos | Whoops Page 106 |
| Steve Withnell | 31/10/2013 17:16:20 |
858 forum posts 215 photos | Hi Geoff,
I do have an excel spreadsheet that calculates all the various parameters. It was on line but the webspace got shut. I'll dig it out and post it here somewhere.
Steve |
| Steve Withnell | 31/10/2013 17:30:32 |
858 forum posts 215 photos | No files folder on the site?
|
| Steve Withnell | 31/10/2013 19:19:32 |
858 forum posts 215 photos |
Not tried this before, but here is a link to the file in my Dropbox: https://www.dropbox.com/s/e1vyhn042t1qth8/Gears_Final_180410.xls
Steve |
| Old School | 31/10/2013 20:14:58 |
| 426 forum posts 40 photos | I have used Steve spread sheet and it is easy to use and the gears I made worked very well.
Oliver |
| Old School | 31/10/2013 20:14:59 |
| 426 forum posts 40 photos | I have used Steve spread sheet and it is easy to use and the gears I made worked very well.
Oliver |
| Geoff Lewis 1 | 31/10/2013 22:00:29 |
| 10 forum posts 12 photos | Many thanks to all you guys who have responded to my query. I move forward another notch. Regards Geoff Lewis |
| Geoff Lewis 1 | 04/11/2013 18:53:28 |
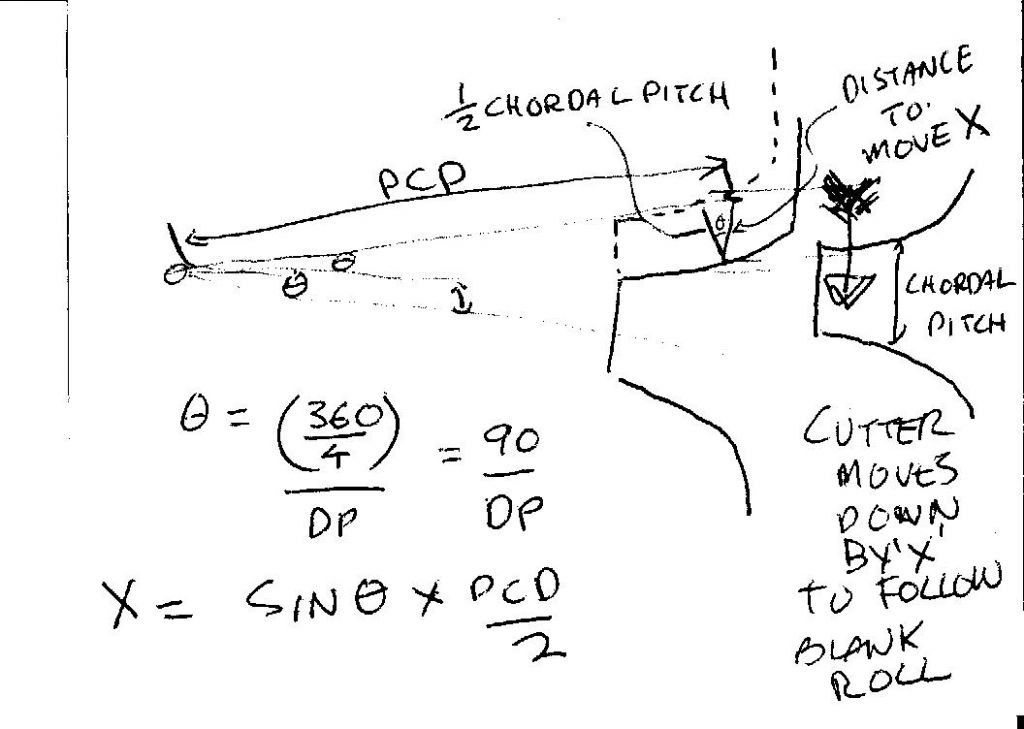
| 10 forum posts 12 photos | I have been looking again at the formula for establishing the movement off the cutter in conjunction with the rotary movemet of the bevel being cut.:- Formula :- Offset = Half Chordal Thickness X 1/2 PCD X SIN Included angle (which in my gears will be 85 & 95 Degs). Can anybody tell me the logic to this formula and how it is derived? I am trying to understand it's physical relationship to the gear being cut and the drawings in Ivan Law's book.
|
| Stub Mandrel | 04/11/2013 21:34:32 |
4318 forum posts 291 photos 1 articles | Hi Geoff, Offset = half chordal thickness = 1/2 PCD X SIN included angle The 'blank roll' is 1/4 of a tooth pitch. The 'chordal thickness' is the distance across a tooth on the PCD i.e. the width of the cutter on the PCD or 1/2 the pitch if the gear was a straight rack). To follow the blank roll around 1/4 of a tooth it has to move by half this distance (chordal width/2) and adjusted for the angle of the blank roll. This angle is where his example of 90/20 comes from 360/4=90 and 20 is the DP of his gear. So imagine a right angled triangle with an included angle theta at the centre of the gear. The hypotenuse is the PCD of the gear and the opposite side is the distance the cutter has to move to keep itself lined up with the small end of the teeth. (Note that PCD must be measured as the true diameter at the small end of the bevel.) As SIn = opposite over hypotenuse the distance the cutter is offset (opposite) = sine * hypotenuse It would have been VASTLY easier to follow if Ivan had used the exactly equivalent formula of: CUTTER OFFSET = SINE (BLANK ROLL) * PCD OF SMALL END OF BEVEL Hope that helps. It has confused the hell out of me. Careful study of the picture on p. 110 helps, or see below. Finally, if you have the courage and the eyesight, you can just execute tha blank roll and very carefully realign the cutter with the small end of the gear - this way you would HAVE to cut the theoretically unnecessary central cut first. Neil
|
| Geoff Lewis 1 | 07/11/2013 16:06:00 |
| 10 forum posts 12 photos | Hi Neil, Many thanks for responding to my latest query. The one thing about it that resonates with me is your remark about it confusing the hell out of you. I identify with that completely. I keep looking at it but still do not see a clear picture. What's throwing me is what 360/4 = 90 has to do with anything. I would have thought that dividing 360/N would have been more likely angle but there you go. I will keep looking at it untill something clicks - or falls off. If you don't hear from me for a while I'm out in the widerness looking for the golden tooth.) I had a rivet but threw it away) Regards Geoff |
| Andrew Johnston | 07/11/2013 22:58:56 |
7061 forum posts 719 photos | Prompted by this thread I've been looking at the design of parallel bevel gears this evening, as I need to produce some bevel gears for the governors on my traction engines. The gears are a bit small for my normal CNC method of producing bevel gears, so I'm planning to use the parallel-depth method. According to my book on gear design the rotation and offset to be used are as follows: 1. Rotate the blank one quarter of the indexing movement required for one tooth space 2. Offset the table by one quarter of the circular pitch at the small end of the teeth Reverse the rotation and offset for the second cut. Intuitively this seems correct and is simple to calculate; no trigonometry required. It does however assume that the indexing required for one tooth space can be exactly divided by four on whatever dividing head is used. Regards, Andrew |
| Michael Gilligan | 08/11/2013 16:17:00 |
23121 forum posts 1360 photos | There was an excellent [and brief] article by R.S. Minchin, in Model Engineer 15-Nov-1964 "Cutting Bevel Gears by the Parallel Depth Method" MichaelG. |
| Stub Mandrel | 09/11/2013 12:17:55 |
4318 forum posts 291 photos 1 articles | Hi Geoff, 360/4 is because you turn by 1/4 of a gear. Neil |
| Stub Mandrel | 09/11/2013 12:20:46 |
4318 forum posts 291 photos 1 articles | Hi Andrew Moving by 1/4 the circular pitch is slightly too far, as CP is measured along an arc of the PCD. Ivan's formula compensates for this (by calculating half the length of a chord joining the ends of an arc of length of half the circular pith!), although it is only really significant for smaller gears, bearing in mind the whole thing is an approximation. Neil Edited By Stub Mandrel on 09/11/2013 12:23:02 |
| Steve Withnell | 09/11/2013 13:09:37 |
858 forum posts 215 photos | https://www.dropbox.com/s/2apmxluzcxph8th/BEVEL%20GEARS.PDF A description of cutting parallel depth bevel gears which I think is far clearer that Ivan Laws book. I should have added that this is from the classic work by Franklin Jones. Steve Edited By Steve Withnell on 09/11/2013 13:13:56 Edited By John Stevenson on 13/09/2015 17:37:56 |
| Geoff Rogers | 09/11/2013 13:45:56 |
| 30 forum posts 4 photos | thank you Steve, both files are most useful In case anyone is interested, I have converted Steve's excel spreadsheet to MathCad (Prime, but can easily be produced in a version 15 option). Why - I just prefer MathCad as I can see all the formula.
|
| Geoff Lewis 1 | 10/11/2013 16:18:45 |
| 10 forum posts 12 photos | Thanks to everybody who has contributed to my queries. I now believe I know where I am going with this. If I don't screw things up in the process I will post some pictures of the result.
Many thanks
Geoff Lewis |
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - Winter Storage Of Locomotives
04/10/2023 21:02:11 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!












 Register
Register Log-in
Log-in


