a little diversion
| Nicholas Farr | 11/10/2021 11:30:51 |
3988 forum posts 1799 photos | Hi, gentlemen the answer is in it's ratio, it is a simple equation i.e. 3+1=4 Circle B stationary = 4 revs of circle A around circle B. Both circles rotating = circle B 1 rev and circle A 3 revs = 4 revs in total of both. Circle A stationary = 4 revs of circle B around circle A Although circle B would come back to the same position at 2 / 3 of a rotation, but not with the same letters aligning as in Macolm's sketch. Regards Nick. Edited By Nicholas Farr on 11/10/2021 11:36:44 |
| Nicholas Farr | 11/10/2021 12:30:40 |
3988 forum posts 1799 photos | Posted by Nicholas Farr on 11/10/2021 11:30:51:
Hi, gentlemen the answer is in it's ratio, it is a simple equation i.e. 3+1=4
Although circle B would come back to the same position at Regards Nick. Edited By Nicholas Farr on 11/10/2021 11:36:44 Hi, I have to correct the above highlighted in bold, it should say one and one third rotations. Regards Nick. Edited By Nicholas Farr on 11/10/2021 13:07:10 |
| not done it yet | 11/10/2021 13:24:00 |
| 7517 forum posts 20 photos | C’mon people . Get sensible. The ration is simply the ratio of the circumferences. Work it out! Think sensibly. How many times do the same size rotate in this scenario? How many times would the smaller circle rotate if the ratio were 2;1? How many on here have worked out gear or pulley ratios and come up with complicated calculations? The answer is three. Nothing complicated, just simple maths where the circumference is proportional to the diameter, the proportionality constant simply being Pi. Circumference of a circle = Pi x Diameter |
| Tony Pratt 1 | 11/10/2021 13:50:59 |
| 2319 forum posts 13 photos | NDIY, well I thought it had to be 3, A @ radius 1, circumference = 6.28, B @ radius 3, circumference = 18.85, everyone do the maths 18.85/6.28 = 3?] Just watched the YouTube video, it looks like it could be 4 Tony Edited By Tony Pratt 1 on 11/10/2021 13:58:01 Edited By Tony Pratt 1 on 11/10/2021 14:04:58 |
| Macolm | 11/10/2021 14:00:36 |
185 forum posts 33 photos | People are not taking this seriously! To consolidate the confusion, what if the small circle rolls inside the large one? Edited By Macolm on 11/10/2021 14:07:49 |
| Tony Pratt 1 | 11/10/2021 14:05:54 |
| 2319 forum posts 13 photos | Macolm, I think people [me] are confused enough as it is. Tony |
| Rod Renshaw | 11/10/2021 14:44:16 |
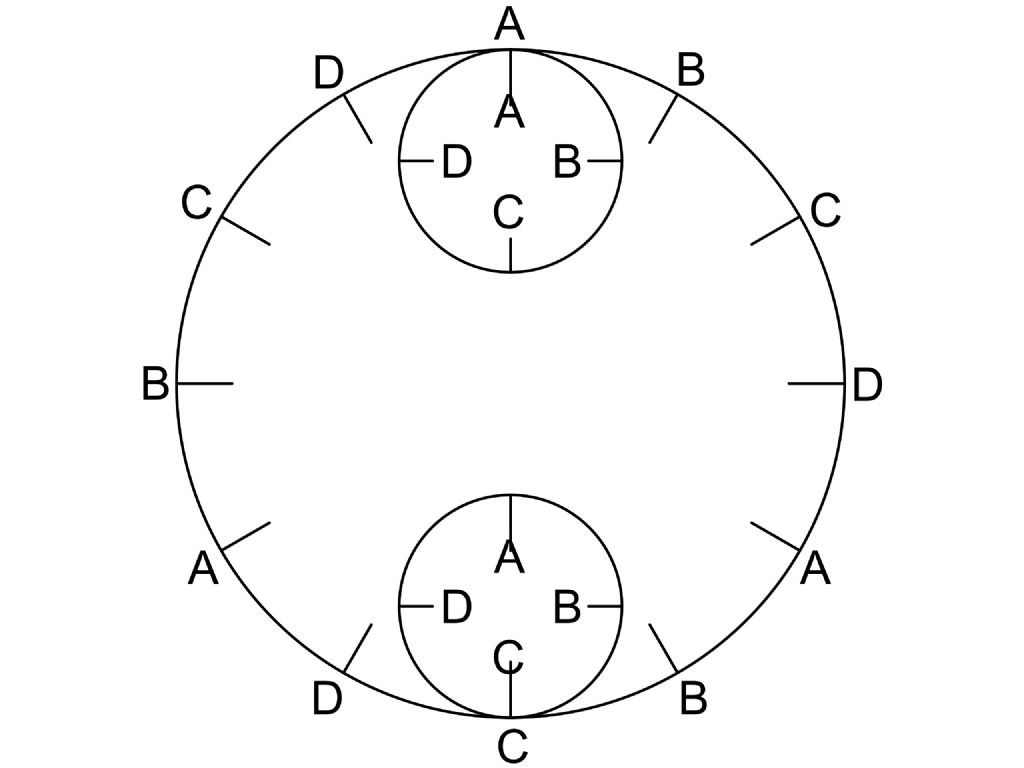
| 438 forum posts 2 photos | Wonderful puzzle. I think I have convinced myself the answer is 4. Malcolm's diagram is very clear. The original question asked was "How many times does the circle "A" revolve in total? and NOT "How many times does the circle "A" rotate about circle "B"? So, A rotates around its own centre 3 times, and A also rotates once around the centre of B. So, 3+1 =4. I think the same argument also applies to the situation where A is inside B. This is one of those situations where one has to concentrate on answering the question as asked. Can't see many at Westminster being able to cope with this. Rod
|
| Tony Pratt 1 | 11/10/2021 14:46:42 |
| 2319 forum posts 13 photos | Final answer is 3, confused no more, I reckon the videos have been spoofed the maths doesn't lie. Just seen Rod's answer, it then becomes a question of interpretation which is a whole different argument & poor question setting. Tony Edited By Tony Pratt 1 on 11/10/2021 14:49:04 |
| Tim Stevens | 11/10/2021 17:10:36 |
1779 forum posts 1 photos | It does seem, as Ron Renshaw suggests, that an O level in any science subject disqualifies anyone seeking election to Parliament. What a state the wonderful traditional public schools and universities have got us into! Sorry, into which they have got us. Tim |
| duncan webster | 11/10/2021 17:26:48 |
| 5307 forum posts 83 photos | Sorry Tony, you're confused, it's definitely 4, and to answer Malcolm's question, 2. |
| Anthony Knights | 11/10/2021 17:35:19 |
| 681 forum posts 260 photos | I'm sorry gentlemen, but it seems obvious to me that the difference between the centres of the the two circles is 3r + r = 4r. What's the problem? |
| Martin Connelly | 11/10/2021 17:37:27 |
2549 forum posts 235 photos | Yes, 4. If you look at Malcom's diagram the small wheel rotates 120° around from the top to the point where the small wheel's A is next to the large wheel's A the small wheel has rotated 1 + 1/3 turns. When it has gone around another 120° to the point where the two A marks are together the small wheel has now done 2 +2/3 turns. By the time it gets back to the top it has done 3 + 3/3 = 4 turns. Martin C |
| Rod Renshaw | 11/10/2021 17:46:52 |
| 438 forum posts 2 photos | This problem gets better or is it worse? After scrolling down David's link following David's suggestion to Michael, I am beginning to think my earlier answer of 4 might be wrong. Is there a difference between "Revolve" and "Rotate"? While it true that Circle A rotates 3 times in it's circuit around Circle B, are any of these "turns" actually revolutions? The poster posits that a revolution means going around something else, a fixed point, and by implication turning on one's own axis is not a revolution. I know we often use these words almost interchangeably, but we can be more precise. The question asks "How may times does Circle A revolve?" Since the only fixed point we have in this line drawing is Circle B, and Circle A only goes around Circle B once, should the answer be !? Any other answers? Rod |
| Peter Greene | 11/10/2021 18:28:16 |
| 865 forum posts 12 photos | You've been reading the original thread, haven't you Rod? |
| Nicholas Farr | 11/10/2021 18:59:10 |
3988 forum posts 1799 photos | Hi Rod, according to my dictionary, both revolve and rotate can be; 1, "to orbit a central point" 2, "to turn on an axis" the term revolution can mean; 1, "orbital motion about a fixed point" 2, "a turning or rotational motion about an axis" so I guess they all mean much the same thing in this context. All three of these words have other definitions as well. Regards Nick. Edited By Nicholas Farr on 11/10/2021 19:00:27 |
| Gary Wooding | 11/10/2021 19:02:40 |
| 1074 forum posts 290 photos | If both circles were the same size, would the right answer be 1 or 2? It's a question of definition, surely. |
| Nicholas Farr | 11/10/2021 19:18:16 |
3988 forum posts 1799 photos | Hi, I don't think anyone is suggesting that the maths are telling lies, and we all know that the circumference of circle B is three times that of circle A and the ratio therefore is three to one, which means there must be four revolutions to a cycle. Circle B is not rotating, but the whole configuration is still a ratio of three to one, and for circle A to complete one cycle, there has to be four revolutions and the only thing revolving is circle A. Regards Nick. |
| Nicholas Farr | 11/10/2021 19:25:58 |
3988 forum posts 1799 photos | Hi Gary, I think it's a case of two for the price of one, as one cycle and one rotation would take place in the same time and space. Regards Nick. Edited By Nicholas Farr on 11/10/2021 19:27:16 |
| Rod Renshaw | 11/10/2021 19:43:15 |
| 438 forum posts 2 photos | Peter - I was reading the 32 nd poster responding to the original post on the Practical Machinist website, and to which I was signposted by David's suggestion to Michael. Are you saying there was a previous thread on this forum, if so I was not aware of it, I was just trying to keep this "diversion" moving. Nick - thanks for the definitions. I was more or less quoting the 32 nd poster I referred to above, and who seemed quite precise and authoritative about his understanding that a revolution must be around a fixed point. As someone has said there may be several answers depending on one's interpretation of the problem and the question. I can't imagine the original question setter could have imagined how much entertainment his/ her question would generate. Rod |
| Martin Kyte | 11/10/2021 22:14:59 |
3445 forum posts 62 photos | 3 rotations and a translation or orbit. Translations are not rotations. regards Martin |
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - Winter Storage Of Locomotives
04/10/2023 21:02:11 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!










 Register
Register Log-in
Log-in


