Constrained Pendulum and Earth Rotation
| roy entwistle | 06/02/2017 11:05:55 |
| 1716 forum posts | Don't forget also that a clock pendulum is considerably shorter than a Foucault |
| Geoff Theasby | 06/02/2017 11:18:07 |
| 615 forum posts 21 photos | OK, Russell, I didn't look up exactly how accurate the very best clocks are. Sorry. Geoff |
| Martin Kyte | 06/02/2017 11:24:26 |
3445 forum posts 62 photos | Yes Russell. I'm only interested in the effect of constraining. Lets just say the distance from the center of mass is a constant. Roy, I did say that. If the periods were the same the pendulum would bob would describe a circle and would not move relative to the escapement (counting device) and the clock would not tick. It has been pointed out to me that the Foucault pendulum precession varies with latitude, something I did not initially recall, although it is clear it must change direction at the equator and vary in a continuous relationship to latitude. This implies that the motion of the mount of a Foucault pendulum affects the bob and causes it to move in an ellipse the minor axis of which varies as the sine of the latitude and is maximum at the pole and zero at the equator. Martin |
| duncan webster | 06/02/2017 12:38:26 |
| 5307 forum posts 83 photos | It is much easier to think about Foucault pendulum at the poles, where the suspension point just rotates once per day. It is rotating about the axis of symmetry of the pendulum swing, I think it is easy to see that it doesn't affect the period of the pendulum. At the equator there is no Foucault effect. This being the case I don't think there is any effect anywhere else. As others have said, the period will be affected by the apparent variaton in g (the accelearation due to gravity) caused by altitude, the oblate shape of the earth, and to a very small degree by centripetal force due to the earth's rotation |
| JA | 06/02/2017 13:20:32 |
1605 forum posts 83 photos | I have not really been following the forum for the last couple of days due to another commitment, a motorcycle show, so I am now catching up on interesting threads. I think only Martin has mentioned the magic phrase "conservation on angular momentum". The Foucault pendulum demonstrates this. If one considers a clock with a free swinging pendulum at one of the poles the direction of swing will change considerably during the day relative to the clock's mechanism. This in itself will give the clock designer serious problems. A balance wheel on a horizontal spindle will have similar problems which, I would suggest, is why Harrison used a pair of opposing torsional balance "weights" on his early chronometers. Later chronometers used a balance on a vertical spindle which gets over this problem. However they may still be effected by Coriolis effects as they move over the surface of the Earth. Again Coriolis forces are the result of the Earth's rotation and conservation of angular momentum. Conservation of angular momentum can become horribly complex particularly with gyroscopes leading to most engineering students switching off when they reach the subject. Highly distinguished learned persons have been known to be total confused by the subject in public, one suggested that gyroscopes had magical powers. I hope that I have got all this right! JA (from his armchair) |
| Russell Eberhardt | 06/02/2017 14:09:47 |
2785 forum posts 87 photos | Posted by JA on 06/02/2017 13:20:32:If one considers a clock with a free swinging pendulum at one of the poles the direction of swing will change considerably during the day relative to the clock's mechanism. This in itself will give the clock designer serious problems.
Not really a problem. They just need to use a suspension which is free in one direction but stiff at right angles to it such as these. The double compound pendulum used in Harrison's ships chronometers was intended to compensate for the rolling movement of the ship not the rotation of the earth. Russell.
|
| SillyOldDuffer | 06/02/2017 14:18:06 |
| 10668 forum posts 2415 photos | Also, from an armchair. I couldn't find anything on the web that directly compares the periods of the two types of pendulum. But I did find an equation for the angular frequency of a Foucault Pendulum that is a modification of that of the standard pendulum. The equations are different, which implies that their periods are also different. Not surprisingly in both equations, the frequency (and therefore period) depends on gravity and the length of the pendulum. The pendulums must be similar, but they are not identical. I am notoriously bad at maths, but I read the Foucault equation as: "the period is determined by the square root of the acceleration due to gravity divided by the length of the pendulum but it is varied + and - by the effects of precession." I think this means that the individual period of each swing of a Foucault pendulum is continually changing. It speeds up and slows down as the earth rotates and I assume the pluses and minuses average out over 24 hours. The 'tick' of a Foucault pendulum is modulated by the rotation of the earth. Or, just as I remember being bemused by spherical geometry at school, am I hopelessly confused again? Help! Dave |
| Martin Kyte | 06/02/2017 14:36:01 |
3445 forum posts 62 photos | I would be handy to know where you found this equation and what omega and lambda refer to. regards Martin |
| JA | 06/02/2017 14:45:03 |
1605 forum posts 83 photos | Russell I think you would need a suspension which is free in both directions for a pendulum to swing successfully at the poles. Granted your comment about Harrison's double pendulum. Dave What are the definitions for the symbols in the equations other than gravity and length? There is some sense in ignoring angular momentum, particularly for the effects it has on one's brain. Those students were right. Now to do something simple, unload the car and go food shopping. JA |
| DrDave | 06/02/2017 14:57:52 |
| 264 forum posts 52 photos | Further to SillyOldDuffer's formulae, I found an interesting derivation of the period of a Foucault pendulum on Warwick University's website. Their final equation is And we are no closer to finding out how a normal pendulum would change frequency with latitude. I would surmise that, because to pendulum is forced to swing in one plane and have no Coriolis acceleration, it should be independent of latitude. Lowers head and prepares to be shot at! |
| SillyOldDuffer | 06/02/2017 15:19:38 |
| 10668 forum posts 2415 photos | Posted by Martin Kyte on 06/02/2017 14:36:01:
I would be handy to know where you found this equation and what omega and lambda refer to. regards Martin Yes, sorry about that Martin. The equation comes from this page at the University of Texas which refers back to this one on Coriolis Force Ω is the 'constant angular velocity about an axis passing through the origin of the inertial frame', and λ defines the angle to the reference frame. As to JA's most excellent suggestion "Now to do something simple, unload the car and go food shopping", I tried that yesterday lunchtime. At about 7pm a neighbour rang my doorbell to ask if knew my car boot had been open all afternoon. Proof that unloading a car is now beyond me too! Dave |
| Martin Connelly | 06/02/2017 15:28:26 |
2549 forum posts 235 photos | Could it be that the unknown variables in Dave's equation are drag from the air which would depend on the configuration of the pendulum and the maximum angle from vertical. As I recall these equations are generally given for ideal pendulums in a vacuum and in the real world the further you go away from very small angles the bigger the difference between theory and practice. The precession of a true Foucault pendulum at a pole is one revolution per sidereal day of 23 hr, 56 min, 4.1 sec. since the earth revolves 366.25 times on its axis each year as viewed from a distant point outside the solar system. It should be noted that the Science museum Foucault pendulum is reset every day and is given an impulse to keep it going that results in a bob motion that is a shallow figure of 8 in the vertical plane. The mechanism was devised by Professor Sir Brian Pippard in 1983. Also details from the Science Museum state that because the Science Museum is not at a pole their pendulum turns slower than once per day with a rotation period of 30 hours and 40 minutes and they also state that at the equator the pendulum would not turn at all. Martin |
| SillyOldDuffer | 06/02/2017 15:47:26 |
| 10668 forum posts 2415 photos | Posted by Martin Connelly on 06/02/2017 15:28:26:
Could it be that the unknown variables in Dave's equation are drag from the air ... Martin No, but that's yet another valid complication to worry about. One of the page links I provided for Martin K mentions that the equations don't account for air resistance. Which leads me into an example of faulty logic. As the earth exists in a very large vacuum, I suggest that drag on the pendulum can be neglected. After all, the average air pressure in our universe must be very close to zero! Interesting that the Science Museum data shows that their pendulum takes over 30 hours to rotate. That's not what I imagined at all. Back to the drawing board - I don't understand it! Dave |
| DrDave | 06/02/2017 17:19:47 |
| 264 forum posts 52 photos | Posted by SillyOldDuffer on 06/02/2017 15:47:26:
Interesting that the Science Museum data shows that their pendulum takes over 30 hours to rotate. That's not what I imagined at all. Back to the drawing board - I don't understand it! Dave Dave, If you look at the bottom of the page that I linked to above, they give the period of rotation as T = 24/sin(latitude). For the Science Museum, this gives T = 24/sin(51.4978) = 30.67 hours. Dave |
| JA | 06/02/2017 17:38:32 |
1605 forum posts 83 photos | The important thing to know here is what "w" is in Dave's Foucault equation. I think DrDave is right. "w" has two components: that for a simple pendulum which is independent of latitude and that due to the period of rotation. To put it another way "w" is the time take for the pendulum, simple or Foucault, to return to the same position. Now someone is going to say "but a Foucault pendulum is a simple pendulum". I just hope we don't meet on a moonless night in a dark ally otherwise the pendulum from my regulator will have a different period. JA |
| John Haine | 06/02/2017 17:50:07 |
| 5563 forum posts 322 photos | Sorry to be pedantic but if by "w" you mean Greek "omega", then it is by convention angular frequency, which equals 2 x pi/period measured in seconds. |
| Neil Wyatt | 06/02/2017 18:10:08 |
19226 forum posts 749 photos 86 articles | Posted by DrDave on 06/02/2017 14:57:52:
Further to SillyOldDuffer's formulae, I found an interesting derivation of the period of a Foucault pendulum on Warwick University's website. Their final equation is And we are no closer to finding out how a normal pendulum would change frequency with latitude. I would surmise that, because to pendulum is forced to swing in one plane and have no Coriolis acceleration, it should be independent of latitude. Lowers head and prepares to be shot at! Wikipedia gives a formula: w = 360 degrees * sin latitude/day the term after sin squared is latitude in your equation. It seems that the rate of the pendulum slows by one swing per rotation, which is one swing per day at the poles, and half a swing per day at 30 degrees latitude (sin 30 = 0.5)
|
| Neil Wyatt | 06/02/2017 18:11:58 |
19226 forum posts 749 photos 86 articles | Just to make things worse, the 'day' is a sidereal day not a solar day as the rotation is relative to the 'frame' of the universe |
| Tim Stevens | 06/02/2017 18:18:04 |
1779 forum posts 1 photos | There may be some confusion here over the different Greek letters. Omega has two forms, normally called (by typographers at least) 'upper and lower case' The upper case is the familiar ohms symbol - a circle broken at the base with short extensions sideways. Lower case omega looks for all the world like a seated generous lady's bottom, from, er, behind. It also resembles a handwriting or italic type small w. The other symbol which looks like a badly written lower-case italic p, is phi - and the upper case version looks like a tall capital I with a fat capital O printed over it. Not that this helps much with Foucaults pendulosities, but at least it gives a clue to how to pronounce them. I think that all pendulums act as Foucaults did, but you can only notice the effect (of change in the line of swing) if the pendulum can swing as it likes, and act for a long time (several minutes at least) without any outside influence to keep it going. This can be achieved easily if you have a very tall building and so can have a very slow moving but heavy bob. Never mind pendulums for a moment, just think about the same effect on the balance wheel of a wrist watch as you play tennis. Other games are available ... Cheers, Tim Edited By Tim Stevens on 06/02/2017 18:19:19 |
| duncan webster | 06/02/2017 19:08:53 |
| 5307 forum posts 83 photos | I'm probably being a bit thick here, but if we go back to the pendulum at the pole, the point of suspension has no linear movement relative to the earth's axis, and so if the suspension has zero rotational stiffness in the axis of the earth's rotation how does the pendulum know that the earth is moving? If the suspension has rotational stiffness it isn't a Foucault pendulum. If the pendulum doesn't know the earth is moving, then that movement can't affect it's period. |
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- hemingway ball turner
04/07/2025 14:40:26 - *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!


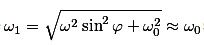
 Neil
Neil









 Register
Register Log-in
Log-in


