Trying to learn about Clock Gears
| Chris TickTock | 22/12/2019 12:44:46 |
| 622 forum posts 46 photos | Hi Guys, In between all the busy things we find ourselves doing at this time of year I am attempting to get a grip on understanding clock gears to eventually be able to machine one and who knows one day even make a clock. The first thing I have learned is that clock gears are not always cucloidal but may be cycloidal or involute or even ogival. Foucusing on a hypothetical starting point of machining a wheel to replace a damaged wheel I already have. What parameters would I need to take from the existing wheel such as tooth pitch etc? i would also be inclined to make my own cutter (I believe I have most equipment for this just need to read the manual etc. I note some old posts mention you have to know the pressure angle which confuses me. Surely if you are generating a shape for the gears (teeth) then the pressure angle will be part of the shape? I suspect then that the pressure angle will determine the shape. An assumption i would make for most gears on a clock excluding the motion work is that they will be a form of cycloid or curve. Any help whatsoever always appreciated. I have and will continue to put a lot of work into this but sometimes a bit of guidance helps a lot. I also have just downloaded inkscape a free cad program which i believe can draw gears. Chris |
| Bizibilder | 22/12/2019 13:16:02 |
173 forum posts 8 photos | Try this book: Book about £30 with no postage to pay. This tells you all you could possibly need to know about clock wheel cutting. There are also clock wheel drawing and calculating programs available on the web - Google will help you. You can buy cutters (which are extremely expensive!!) or make your own - which is quite easy to do, especially after a bit of practice. Forget pressure angles and involute curves - these do not apply to clock wheels or pinions. Edited By Bizibilder on 22/12/2019 13:17:27 |
| Brian H | 22/12/2019 13:19:20 |
2312 forum posts 112 photos | Thee is a vast difference between engineering gear that need to transmit power and clock gears that need minimum friction and are rarely used at high revolutions. I confess to being an engineer, albeit a quality one but I've also made a clock and repaired several. There is no mention of pressure angle in a couple of horological books that I have, nor in an old MAP (Model Engineer) book on gear wheels and gear cutting. Hopefully, someone who knows what they are talking about will be along shortly with some useful advice but I suspect that you are correct in going for cycloidal tooth forms. Brian |
| Michael Gilligan | 22/12/2019 15:07:28 |
23121 forum posts 1360 photos | You might find this useful, Chris : **LINK** http://www.delphelectronics.co.uk/gcode.htm ... and this of interest : https://www.csparks.com/watchmaking/CycloidalGears/index.jxl [ be sure to follow the embedded links on that page ] MichaelG. Edited By Michael Gilligan on 22/12/2019 15:17:20 |
| David Noble | 22/12/2019 15:12:32 |
402 forum posts 37 photos | Posted by Bizibilder on 22/12/2019 13:16:02:
Try this book: Book about £30 with no postage to pay. This tells you all you could possibly need to know about clock wheel cutting. Brilliant book, all the information that you will need is there. David |
| SillyOldDuffer | 22/12/2019 15:13:47 |
| 10668 forum posts 2415 photos | Posted by Chris TickTock on 22/12/2019 12:44:46:
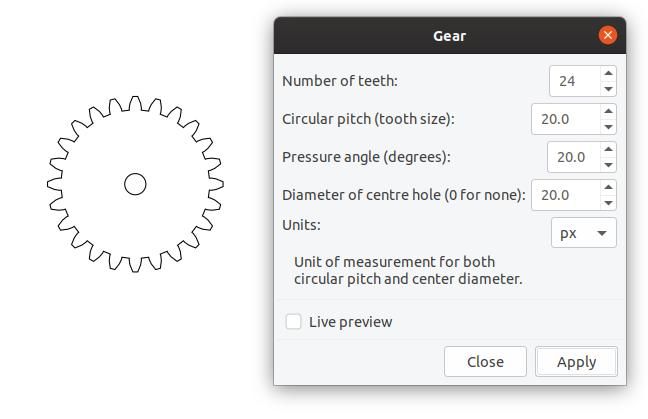
Hi Guys, In between all the busy things we find ourselves doing at this time of year I am attempting to get a grip on understanding clock gears to eventually be able to machine one and who knows one day even make a clock. The first thing I have learned is that clock gears are not always cucloidal but may be cycloidal or involute or even ogival. Foucusing on a hypothetical starting point of machining a wheel to replace a damaged wheel I already have. What parameters would I need to take from the existing wheel such as tooth pitch etc? i would also be inclined to make my own cutter (I believe I have most equipment for this just need to read the manual etc. I note some old posts mention you have to know the pressure angle which confuses me. Surely if you are generating a shape for the gears (teeth) then the pressure angle will be part of the shape? I suspect then that the pressure angle will determine the shape. An assumption i would make for most gears on a clock excluding the motion work is that they will be a form of cycloid or curve. Any help whatsoever always appreciated. I have and will continue to put a lot of work into this but sometimes a bit of guidance helps a lot. I also have just downloaded inkscape a free cad program which i believe can draw gears. Chris Inkscape can draw Involute gears and racks by following the menu Extensions->Render->Gear. The dialogue and gear it drew is shown below: The teeth are sized and shaped to engage with another gear of the same specification, this boiling down to the numbers entered in the dialogue. Almost all modern gears are involute because they are smooth running, not effected by small spacing errors, and are easy to mass produce. Most gears are used to transmit power, and the involute form is said to be good for this - low wear, whilst careful shaping of the teeth reduces gear whine at speed. Typically a fast rotating power source is geared down to drive road wheels or a machine. Clock gearing is arranged the other way round: a very slow turning drum powered by a spring or weight gears up to turn a relatively fast moving seconds or minute hand. Somewhere near the top of the gear train, an escapement connected to an accurate timer like a pendulum, allows the train to tick in timed steps, perhaps once per second. These ticks are divided down through another gear train to show HH : MM : SS. As clocks don't have power to spare its important to minimise friction. Cycloidal gears are said to be better for low friction than involutes, but it's not clear to me why. My admittedly weak understanding suggests involute gears should be best for everything. Early clock-makers knew sod-all about involutes and cycloids! Their clocks were built by eye and experience. The experience comes from looking at worn teeth, perhaps in a local water mill, because teeth tend to grind down naturally to matching curves. Craftsman copied these curves with a file to cut new teeth, avoiding the running in stage. Later on mathematicians did a proper analysis and produced the formulae needed to shape properly matching gears from first principles. One way of making clock gears is to carefully grind a tool to fit the profile of an existing gear. (This may be essential when repairing a very old clock.) Then, with the gear blank held in a dividing head, the tool can be spun like a fly-cutter to chop teeth one by one around the circumference. A posh dividing head isn't necessary - people use old saw blades to provide the necessary indexed steps. Making tools to cut mathematically defined curves is more challenging. Ivan Law's Gears and Gear Cutting is a good place for practical men to start - I've found the maths in engineering textbooks very difficult. You could also grind tools to match gears drawn by Inkscape. Most professional gears are made by hobbing, where a specially shaped cutter and blank are synchronised together. Or gear cutters can be bought to match the required DP(Imperial) or Modulus(Metric) : quite a lot of them may be needed. Ivan Law describes a method using buttons, and a more modern idea produces the curves by facing the new tool into the side of a cone drill. The only method I've used is this medieval home-made tool, which, despite it's crude appearance generates involutes that fit Meccano. Hours of fun ahead! Dave Edit: Poxy Smileys! Edited By SillyOldDuffer on 22/12/2019 15:16:27 |
| Tim Stevens | 22/12/2019 15:28:41 |
1779 forum posts 1 photos | If you look at the examples in Michael Gilligan's link, you will see that the first is an involute gear (tables on the right side) with the pressure angle specified, while the third example is cycloid and the area in the table is grey. This is because cycloid gears are created by a different method and the actual pressure angle (and some other details) can vary depending on which bit of the tooth you are looking at. It does not seem to be clear why clock makers use cycloid gears, - I suspect that tradition, and inheriting a box of old cutters, are both good reasons. It may also be that as the pivots wear - a likely outcome in a 50 year old clock never cleaned or oiled - that a cycloid design is more tolerant of the extra slack. Hope this helps - Tim |
| Michael Gilligan | 22/12/2019 15:33:29 |
23121 forum posts 1360 photos | Posted by Michael Gilligan on 22/12/2019 15:07:28: . [ be sure to follow the embedded links on that page ] MichaelG. . ... especially this one : Finally, I would like to mention a privately published monograph by my gear-expert friend, Richard Thoen. This work explains why, in his opinion, cycloidal gearing belongs entirely in the dust-bin of history. MichaelG. |
| Chris TickTock | 22/12/2019 16:54:13 |
| 622 forum posts 46 photos | Thanks for posts to date all really helpful. Firstly I think my plan of attack will be to make a copy of an existing brass wheel to get some experience grinding my own cutters and get familiar with my equipment.. For most clock repair work involving making a damaged wheel I suspect this would be the way to go. Apparently many clock profiles described as cycloid may be ogival and not an epicycloid but curves. In fact I think there is a standard used which stipulates various appedundrum curves. The question I need answering still is when should or in practical terms would a clock maker use cad to form the gear profile as opposed to either rule of thumb or just copying another. Chris |
| roy entwistle | 22/12/2019 21:15:25 |
| 1716 forum posts | Chris Remember that mostly on a clock it's the wheel which drives the pinion. Which is not the most efficient situation. Roy |
| Chris TickTock | 22/12/2019 21:55:11 |
| 622 forum posts 46 photos | Posted by roy entwistle on 22/12/2019 21:15:25:
Chris Remember that mostly on a clock it's the wheel which drives the pinion. Which is not the most efficient situation. Roy I take it you refer to clocks generally stepping up the speed through its gearing. Why is this more inefficient than stepping down? Chris |
| SillyOldDuffer | 22/12/2019 22:14:01 |
| 10668 forum posts 2415 photos | Posted by Chris TickTock on 22/12/2019 16:54:13: ... Apparently many clock profiles described as cycloid may be ogival and not an epicycloid but curves... The question I need answering still is when should or in practical terms would a clock maker use cad to form the gear profile as opposed to either rule of thumb or just copying another. Chris Not sure I understand the first sentence. Aren't cycloids and epicycloids particular curves with mathematical definitions, whereas 'ogive' is just a general description of any pointy shape like an arch or tooth? Likewise, there are lots of different curves, pretty much anything other than a straight line. I'm sure clock teeth could be made of unscientific ogives and curves and still work, but they're unlikely to be low friction. A clock made of substandard gears would wear faster and need more power to drive it reliably. It might need so much power that pinions carve or bend. CAD has the advantage of producing properly designed gears without any need to understand the rather difficult theory or do the necessary number crunching and drawings. Guessing is eliminated. In contrast Rule of Thumb and copying other gears is comparitively hit and miss. Why blunder about in the dark when an electric light is available? Dave |
| not done it yet | 22/12/2019 22:24:03 |
| 7517 forum posts 20 photos | anything other than a straight line. Even a straight line is a curve, is it not? Just one of infinite diameter? |
| John Haine | 22/12/2019 22:51:05 |
| 5563 forum posts 322 photos | You can use CAD to draw a profile, but forming it in metal is quite another issue! Involute gears can be generated by a "rack form" cutter, which has straight edges, usually by hobbing. But If you want to hob "cycloidal" gears then the hob has to have a complex curved shape which just moves the problem of making a precise complex curve from the gear to the cutter. Approximations to involute teeth can just use circles instead of the true involute - cutters for this can be made by the "two button" method. It is also possible to CNC turn the precise shape into the cutter profile, which could be done for both involute and "cycloidal" teeth. This shows the tooth form of a "two-button" type cutter (circular approximation to involute) being formed by CNC on a form-relieving fixture in my lathe. It would be just a matter of having the right equation to make a cycloidal type cutter. |
| Michael Gilligan | 22/12/2019 23:03:17 |
23121 forum posts 1360 photos | Posted by Chris TickTock on 22/12/2019 16:54:13:
.Apparently many clock profiles described as cycloid may be ogival and not an epicycloid but curves. In fact I think there is a standard used which stipulates various appedundrum curves. […] . Just a reminder, Chris ... On your recent ‘pinion wire’ thread, I posted a relevant link. ... if you need more than that, I recommend reading ‘Gears for Small Mechanisms’ MichaelG. . . Posted by Michael Gilligan on 14/12/2019 08:58:50: . The standard profile is described in BS 978 part 2 . Not sure if this **LINK** really counts as an ‘extract’ but anyway ... MichaelG. |
| Hopper | 22/12/2019 23:44:12 |
7881 forum posts 397 photos | Posted by Chris TickTock on 22/12/2019 16:54:13:
The question I need answering still is when should or in practical terms would a clock maker use cad to form the gear profile as opposed to either rule of thumb or just copying another. Chris CAD is only for making gears for digital clocks. Grinding a tool to match your existing good gear would get the job done, for this one-off repair job. Modern technology is a wonderful thing but often cruder olde-worlde methods are quicker and simpler in the home workshop. |
| Michael Gilligan | 22/12/2019 23:45:56 |
23121 forum posts 1360 photos | Posted by SillyOldDuffer on 22/12/2019 22:14:01: […] whereas 'ogive' is just a general description of any pointy shape like an arch or tooth? […] . I stand to be corrected, Dave ... but, as I understand it, the ogive is formed by the intersection of two equal circular arcs of radius greater than the width of the arch [or in this case, tooth] MichaelG. |
| Bazyle | 23/12/2019 00:25:56 |
6956 forum posts 229 photos | Involute gears provide 'constant velocity ratio' in transmission, so no variations in speed transmitted which in say a car gearbox would cause vibration. They do this at the expense of the faces sliding over one another which means friction and loss of power. Final question of when would a clockmaker use CAD to form the teeth etc. Answer Never. A clockmaker would use CAD to layout the positions of wheels and pinions and general design but would never draw actual gear teeth just circles to show the position to avoid hitting pillars etc but the teeth don't need drawing just making using the normal methods. An engineer would draw such teeth because they are more interested in playing with the toy than making a clock. |
| Sam Stones | 23/12/2019 04:12:50 |
922 forum posts 332 photos | Bazyle, I resemble that remark |
| Hopper | 23/12/2019 05:20:25 |
7881 forum posts 397 photos | Posted by Bazyle on 23/12/2019 00:25:56:...
... An engineer would draw such teeth because they are more interested in playing with the toy than making a clock.
You left out the word "armchair". |
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- hemingway ball turner
04/07/2025 14:40:26 - *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!












 Register
Register Log-in
Log-in


