diameter calculation
| paul rayner | 10/10/2019 21:09:38 |
| 187 forum posts 46 photos | Hi all I'm wanting to drill 3 holes in a triangular fashion on my mill with the PCD function I've already set up the work piece with the quill in the centre, The centre of the holes are 65mm equally distant apart from each other. Question is how do I calculate the diameter of the circle needed? I could do it on paper with a compass etc but I want it more accurate than that. I've had a look at the machinery's manual but cannot seem to find anything. thanks in advance for any help regards Paul |
| Nicholas Farr | 10/10/2019 21:21:12 |
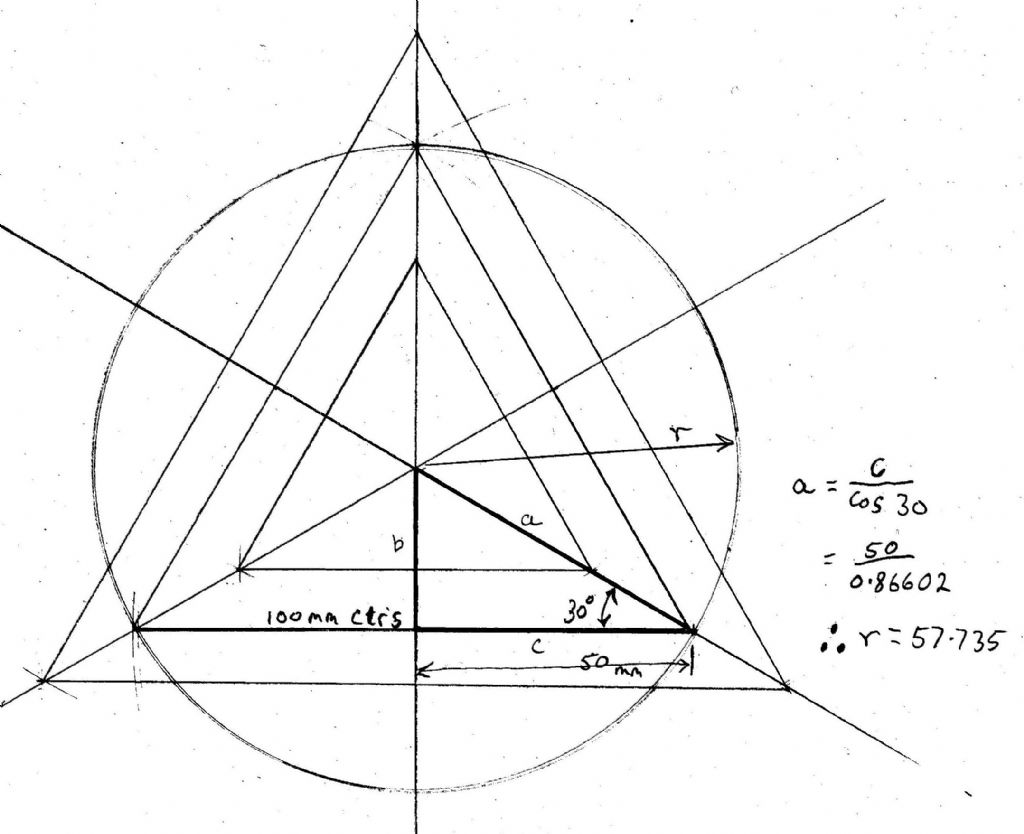
3988 forum posts 1799 photos | Hi Paul, a little bit of Trigonometry will give you the answer, just substitute the 100 shown on the diagram below with 65. Regards Nick. Edited By Nicholas Farr on 10/10/2019 21:21:47 |
| vintage engineer | 10/10/2019 21:21:44 |
293 forum posts 1 photos | I will work it out in cad for you. I make it 75.12mm diameter.
Edited By vintage engineer on 10/10/2019 21:37:15 |
| paul rayner | 10/10/2019 21:37:08 |
| 187 forum posts 46 photos | Thanks Guys just the job, I will plot it out First job in the morning. regards Paul |
| not done it yet | 10/10/2019 22:26:15 |
| 7517 forum posts 20 photos | I make it only 75.06mm, not that it is likely to make any difference at all. |
| DMB | 10/10/2019 22:46:33 |
| 1585 forum posts 1 photos | I prefer Nick's answer. Why 3 diff? |
| Michael Gilligan | 10/10/2019 23:07:38 |
23121 forum posts 1360 photos | ndiy seems to be closer MichaelG. |
| Mike Poole | 10/10/2019 23:15:21 |
3676 forum posts 82 photos | 75.0555349947 for rough work Mike |
| Nicholas Farr | 10/10/2019 23:41:40 |
3988 forum posts 1799 photos | Hi Mike, have you been using my calculator? Regards Nick. |
| not done it yet | 11/10/2019 08:01:03 |
| 7517 forum posts 20 photos | To be honest, as a mathematician one would only quote the result as 75mm - as one cannot provide an answer to more significant figures than the data supplied with any confidence. That 65 value could be anywhere between 64.50 and 65.49 (extra significant figures shown to demonstrate the validity of the result after rounding to 3 sig. figs.). Had it been measured to greater precision, like 65.00mm, a more precise result could be provided with confidence. In practice the result for 65mm could be anywhere between 74.5mm and 75.6mm. Hence 75mm, to 2 significant figures, is really the best one can offer. Remember, the average of 1 and 2 is 2, but the average between 1.0 and 2.0 is 1.5. We often provide answers to greater precision than the real world measurements deserve! Edited By not done it yet on 11/10/2019 08:02:52 |
| Mike Poole | 11/10/2019 08:08:00 |
3676 forum posts 82 photos | Obviously as a Myford user working to ten decimal places is normal practice Mike Edited By Mike Poole on 11/10/2019 08:08:17 |
| Nicholas Farr | 11/10/2019 08:31:12 |
3988 forum posts 1799 photos | Hi NDIY, the OP asked the diameter for 65mm without stating a tolerance of any kind. The mathematical answer is exacting within the practicalities of calculation and from that the OP can fashion his own tolerance and I'm sure he should be able to get it very close to his needs. Regards Nick |
| paul rayner | 11/10/2019 08:31:22 |
| 187 forum posts 46 photos | 75.06 will do for my needs thank you for all your help, It was a head scratcher for me! regards Paul |
| Michael Gilligan | 11/10/2019 08:46:10 |
23121 forum posts 1360 photos | Posted by not done it yet on 11/10/2019 08:01:03:
[…]
We often provide answers to greater precision than the real world measurements deserve! .
That said; it does no harm to declare a theoretical target value, provided that you understand that reaching it may be impractical.
. Best I could get last night was: (( 32.5 ÷ 0.866025403784 ) x 2 ) = 75.05553499468936
|
| SillyOldDuffer | 11/10/2019 09:06:46 |
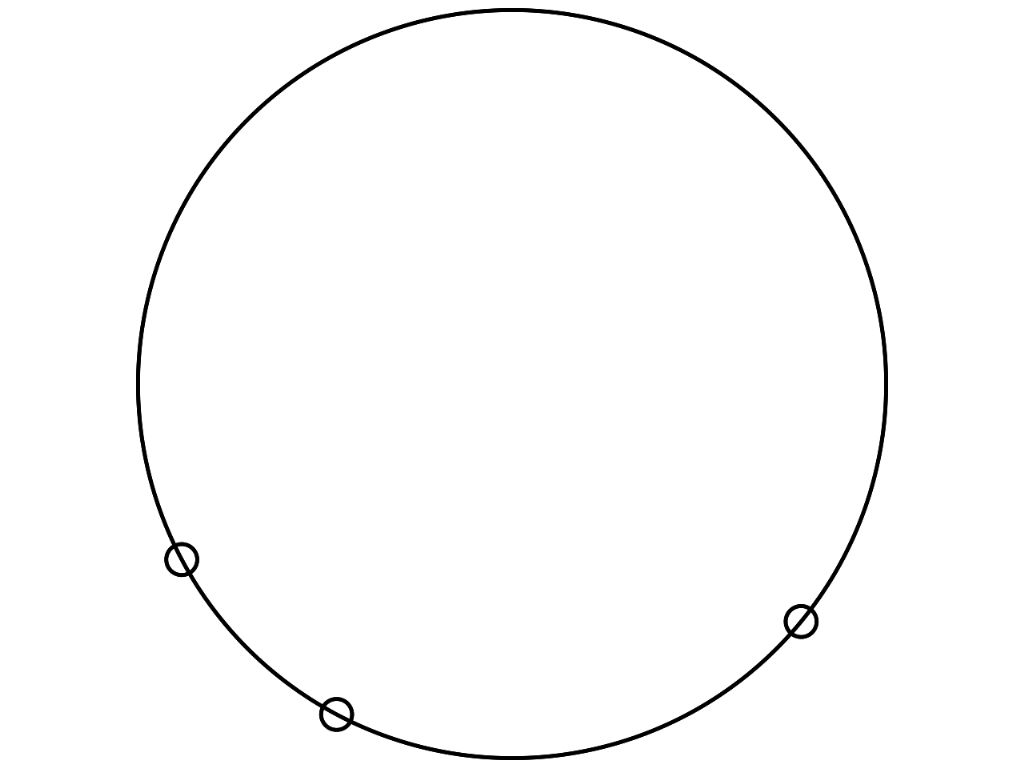
| 10668 forum posts 2415 photos | Nick's excellent solution is for the simple case ie a circle defined by three points of an equilateral triangle. What's the solution when the circle is defined by 3 randomly placed points? A mathematical solution must be possible: I drew the example above with QCAD, but most other CAD packages can draw circles specified by three points. Please be gentle - maths doesn't come naturally to me... Dave |
| Michael Gilligan | 11/10/2019 09:20:30 |
23121 forum posts 1360 photos | I’ve got that tucked-away somewhere, Dave ... it’s quite elegant. I will post it later, if no-one beats me to it. MichaelG. .
Just search for ‘perpendicular bisector’ Edited By Michael Gilligan on 11/10/2019 09:24:10 |
| Andrew Johnston | 11/10/2019 09:28:46 |
7061 forum posts 719 photos | Posted by SillyOldDuffer on 11/10/2019 09:06:46:
A mathematical solution must be possible Simples! The Equation of a circle has three unknowns. Three unique points give you three indpendent equations. Three equations and three unknowns allows a unique solution for the centre and radius, with a bit of algebraic manipulation. Andrew |
| Nicholas Farr | 11/10/2019 10:05:06 |
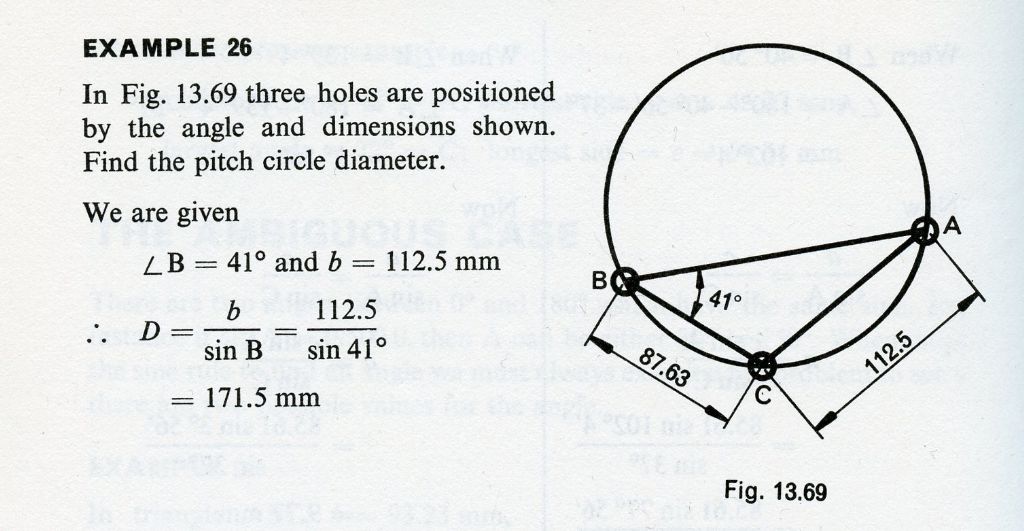
3988 forum posts 1799 photos | Hi S.O.D., I've found this in one of my books, but it does give a couple of dimensions and an angle, but you've asking about random placed points and I suspected it would involve Algebra as Andrew has said. However I could never get to grips with Algebra, which seems that MichealG's search is full of. Regards Nick. |
| Kiwi Bloke | 11/10/2019 10:06:06 |
| 912 forum posts 3 photos | I'd do it using co-ordinate geometry. Not sure if this is what Andrew is suggesting. I'm a lousy mathematician, and I bet there's a far easier way (no, not CAD). The perpendicular bisectors of two chords intersect at the circle's centre. You can easily find the co-ordinates of the mid-point of a chord and its slope. The equation of the bisector of the chord follows, straightforwardly. It's then a few small steps to solve the two equations of the two chord bisectors, to get the co-ordinates of the centre. The diameter is the distance from the centre to any of the three points. The equation for the circle follows. Incidentally, the radius of the circumcircle of a triangle, R = a / 2 * sin A, where a is the length of the chord opposite the angle (vertex) A. Sometimes useful... Oh, Nick just beat me to it... Edited By Kiwi Bloke on 11/10/2019 10:07:27 |
| Michael Gilligan | 11/10/2019 10:44:28 |
23121 forum posts 1360 photos | Posted by Nicholas Farr on 11/10/2019 10:05:06:
[…] Algebra, which seems that MichealG's search is full of. . Oh dear ... maybe this will help: **LINK** http://mathworld.wolfram.com/PerpendicularBisector.html MichaelG. . Edit: or this : http://tgbasics.weebly.com/construct-a-circle-given-3-points.html Edited By Michael Gilligan on 11/10/2019 10:48:42 |
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - Winter Storage Of Locomotives
04/10/2023 21:02:11 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!










 Register
Register Log-in
Log-in


