Electronic Indexers - How Is Cumulative Error Avoided?
| William Chitham | 30/05/2019 12:22:08 |
| 156 forum posts 56 photos | I am planning to build an electronic indexer, initially to make a 127-135 tooth compound gear for my Boxford. Am I right in thinking that the normal way for the programming to work is for the controller to divide 360 by the number of teeth, round the result to whatever number of discrete steps the stepper/drive ratio can manage and apply that repeatedly to the work on the assumption that the error will be insignificantly small? My concern is that the error is cumulative from tooth to tooth and therefore all delivered together on the last tooth. Furthermore the error is proportional to the diameter of the blank. Since I want to cut gears with lots of teeth, a comparitively large diameter and a prime number of teeth to boot the error is going to be enough to make the gear useless. For instance if the error per tooth is .01% then by the time I get to 135 teeth it will be 1.35%. The diameter is around 190mm, circumference approx 597mm so the cumulative error is going to be 8mm. I know many people have successfully built and used these things so I suppose there must be something wrong in my understanding of the principles, can anyone enlighten me? Thanks, William. |
| duncan webster | 30/05/2019 12:54:43 |
| 5307 forum posts 83 photos | There was a thread on here before about this, in brief it's done by a bit of nifty integer arithmetic which keeps track of the error, and makes a move one step bigger or smaller now and again to compensate. Far and away the easiest is to use Silly Old Duffer's software and an Arduino. I can supply stripboard layout if you want to use a Nano cheaper than UNO and has soldered connections, more reliable than plug in) see my post of 15/04/2019 14:01, I can send more photos if you wish |
| Bazyle | 30/05/2019 13:13:07 |
6956 forum posts 229 photos | The solution is to do each calculation individually ie calculate for 1/127, then 2/127, then 3/127. If the fun is in making an electro-mechanical gizmo then go for it. If you don't like electronics then go for an old school differential indexing device. |
| Mike Crossfield | 30/05/2019 13:43:58 |
| 286 forum posts 36 photos | I built Steve Ward’s excellent design of controller a few years ago. Very well documented and simple to build using a programmed PIC and pcb available from Steve at very low cost (Full kits also available). Regarding William’s original question, Steve answered this with respect to his own design in response to someone else’s question a few years ago. I quote:
“So basically internally it multiplies the number of divisions by the actual division its on then divides the result by the number of steps for a full circle - this gives it the nearest number of steps it needs to get to that division (doing the multiply first prevents loss of resolution although it means it needs 32 bit maths which is why the max steps per rev is 16 bit). HTH |
| John Haine | 30/05/2019 13:49:16 |
| 5563 forum posts 322 photos | Even easier is to buy the indexer kit from "World of Ward". Processor comes ready programmed. Several posts elsewhere on this site about it. Photos of mine in my "Digital Dividing head" album. |
| Andrew Johnston | 30/05/2019 14:24:17 |
7061 forum posts 719 photos | I wrote up a similar method to that elucidated by Mike, and then lost it before posting due to finger trouble. If I were doing something similar to the OP I wouldn't muck about with integer arithmetic. I'd choose a processor with a floating point unit; makes life so much easier. Andrew |
| SillyOldDuffer | 30/05/2019 15:59:07 |
| 10668 forum posts 2415 photos | As I recall in the earlier discussion (can't find it!), I started by arguing that the error was insignificant, but was soon persuaded it was worth correcting. (Accumulating error might become significant particularly if a coarse stepping motor drives a rotary table with a low ratio worm.) Bressingham was suggested, but I settled for a simple averaging process that distributes the error around the circumference rather than letting it accumulate so that one tooth in a gear is malformed. The maths came from Duncan (many thanks!) and the code is: nextSteps = ( (long)(divisionStepCount+1) * motorSteps + (long)rstatus.divisionSteps/2 ) / (long)rstatus.divisionSteps; motorSteps is the number of micosteps needed to turn the rotary table through one revolution. It takes the table's worm ratio into account and the motor's base step (usually 200), and the motor controllers microstep setting. rstatus.divisionSteps is the user request (ie the number of gear teeth wanted), and divisionStepcount is how far the turn has got so far. nextSteps is the number of microsteps the motor will be sent to step the rotary table to the next position; thanks to the maths the number of microsteps jitters very slightly around the correct position on each division as necessary to share any error equally throughout the turn. No error, no correction applied. Bottom line: if there is an error it will be small, it is shared out to minimise the effect, and it does not accumulate. Because stepper motors are themselves integer devices there's not much advantage in using floating point arithmetic which uses more memory and is relatively slow. However although all the numbers needed to control the motor are stored as 16 bit integers, Duncan's calculation is done at 32 bit precision to avoid overflow. Dave
|
| William Chitham | 30/05/2019 16:07:36 |
| 156 forum posts 56 photos | Thanks all, thought there must be more to it. I'd arrived at both the solutions described by muddling around with a spreadsheet but I don't have enough understanding of code to see the sums in the various versions that I've looked at. William. |
| SillyOldDuffer | 30/05/2019 16:24:56 |
| 10668 forum posts 2415 photos | Posted by William Chitham on 30/05/2019 12:22:08:
... Am I right in thinking that the normal way for the programming to work is for the controller to divide 360 by the number of teeth, round the result to whatever number of discrete steps the stepper/drive ratio can manage and apply that repeatedly to the work on the assumption that the error will be insignificantly small? ...
Not quite. You're on the right track except the motor and controller don't work in degrees. A typical stepper motor does 200 'natural' steps of per rotation or 1.8° per step. However the fiendishly clever motor controller can subdivide each natural step, at the extreme up to 250000 steps per revolution or about 0.0014° per step. There's a trade off between speed and accuracy. It takes forever to spin a motor at 0.0014° per step. In practice I run my controller at 0.1125° per microstep (200x16), and that's fed into a 90:1 worm on the rotary table, giving 0.00125° per step at the job. The software does the maths necessary to translate user needs in degrees or divisions at the table into microsteps at the motor controller. Dave
|
| Andrew Johnston | 30/05/2019 16:50:04 |
7061 forum posts 719 photos | Posted by SillyOldDuffer on 30/05/2019 15:59:07:
......there's not much advantage in using floating point arithmetic which uses more memory and is relatively slow.
Oh dear Dave, you're a bit behind, although at least in the 20th rather than the 19th. By chance I'm looking at a processor for a design update on a CO2 gas sensor board at the moment. The preferred processor has an ARM Cortex M4 core with a full implementation of the IEEE754 single precision floating point specification. Floating point addition, subtraction and multiplication are all single cycle operations. At the maximum clock rate of 72MHz that's about 14ns. One off price of the processor from Farnell is under £4. What's not to like? Andrew |
| Neil Wyatt | 30/05/2019 16:54:44 |
19226 forum posts 749 photos 86 articles | The other way is to use a variation on the Bressingham Line Algorithm, treating one rotation and the number of holes as analogous to X and Y displacement along a line. Much easier and works by minimising the absolute error at each step Neil |
| Andrew Johnston | 30/05/2019 17:13:41 |
7061 forum posts 719 photos | Posted by Neil Wyatt on 30/05/2019 16:54:44:
The other way is to use a variation on the Bressingham Line Algorithm............ Must have steam on the brain - it's actually the Bresenham line algorithm. Andrew |
| Robert Atkinson 2 | 30/05/2019 17:47:24 |
1891 forum posts 37 photos | While microstepping improves torque ripple and position overshoot, it does not necessarily provide improved positional accuracy. This is particuarly true ff the load (torque) is variable. Performance depends on the motor, controller and load. It's easy to get caught up in the numbers but the whole system must be considered or you may be wasting effort for no real improvement. Robert G8RPI. |
| SillyOldDuffer | 30/05/2019 17:51:49 |
| 10668 forum posts 2415 photos | Posted by Andrew Johnston on 30/05/2019 17:13:41:
Posted by Neil Wyatt on 30/05/2019 16:54:44:
The other way is to use a variation on the Bressingham Line Algorithm............ Must have steam on the brain - it's actually the Bresenham line algorithm. Andrew Must be catching - I spelt Bresenham wrong too! M4 Cortex for £4! Even though I'm totally loyal to all things Arduino that's got to be worth a look! Dave
|
| Bazyle | 30/05/2019 18:10:34 |
6956 forum posts 229 photos | In practice the problem has quite a low boundary. You are only ever going to cut gears up to 200 (plus whatever the JW large wheel skeleton uses) so the number of variables is quite small. For each of those 200 you need a maximum of 200 entries, average 100, in a table telling you how many steps to take. So the memory requirement is only 200x100 off 16bit numbers. You can do the calculations in excel and blow them into an eprom (except nobody does that anymore) have a few switches on the high address lines to select the tooth count and a couple of counters take the values and do the steps. No processors needed ! |
| Alan Vos | 30/05/2019 18:10:53 |
| 162 forum posts 7 photos | Posted by Bazyle on 30/05/2019 13:13:07:
The solution is to do each calculation individually ie calculate for 1/127, then 2/127, then 3/127. That. The one time I did stepper motor control the basic logic was: For fast movement, consider acceleration and deceleration rather than going straight to full speed followed by a hard stop. That allows a smaller motors to deliver higher speed without missed steps. |
| Joseph Noci 1 | 30/05/2019 18:51:00 |
| 1323 forum posts 1431 photos | Posted by Neil Wyatt on 30/05/2019 16:54:44:
The other way is to use a variation on the Bressingham Line Algorithm, treating one rotation and the number of holes as analogous to X and Y displacement along a line. Much easier and works by minimising the absolute error at each step Neil Precisely what I did with my ELS implementation and Electronic gear hobber - both sort of described in my various posts on MEW ( How I link to them is anyone's guess, or maybe Neil's...) Bresenham takes care of it all with the smallest errors possible, and I used the Nucleo range of STM processor modules - Arduino lookalike/workalike, only MUCH faster , 140MHz, floating point, and US$15.00 for a board, with its programmer module..As Andrew said, whats not to like??? Mips/floating point, etc, are all VERY inexpensive today and while it's great to obfiscuricate software skills in retro-capability processors, why bother... Bresenhams works very well in ALL these applications. But, this is all intellectual masturbation if the OP just simply wants a system that he can apply and get to work, especially if he is not that able in the software space. In which case, I would suggest obtaining one of the mentioned systems that already work, and are more a diy assembly project than an adventure... Joe
|
| Massimo Dalmonte | 31/05/2019 07:31:45 |
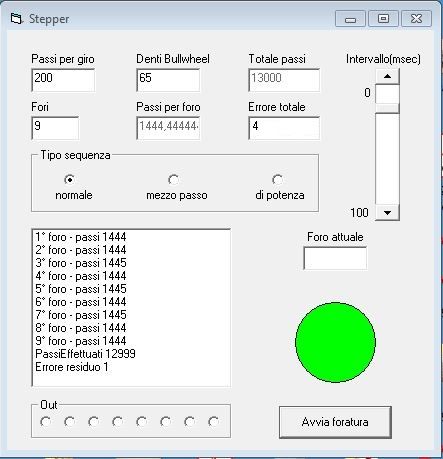
| 33 forum posts 18 photos | Ten years ago, though I didn't have a specific need, I liked very much the idea of the J.A.Radford headstock indexing attachment and thought of putting a stepper motor on its worm shaft to spin it. The stepper would be driven using an old laptop via the parallel port () and I made a small Visual Basic program, using a DLL (IOPort.dll, I think to recall) to output the signals ( these had to be "strengthened" in some way before sending them to the motor, naturally).
Here is an example of how it worked: the three input data are: - motor steps per revolution: 200 - bullwheel teeth: 65 (I own an ML10) - holes to be drilled\teeth to be cut (9 in this case) Dividing 13000 steps by 9, gives 1444.4 period, so each position will be 1444 steps apart from the previous one, and we will have to spread 4 "orphan" steps on the whole revolution (this is done 3 times, on holes\teeth 3,5 and 7, the 4th step is not added, though now I see that it could be added to the first or the last step...). Hitting the button started the sequence, the 8 outputs to the Data pins of the port were monitored in the Out frame, the DLL provided a choice of the kind of sequence used to drive the motor and it was possible to change the interval between one sequence and the next, to adapt it to the stepper. As with a lot of my projects, I didn't proceed further with the hardware part, due to lack of time, but who knows... (today I think the motor command part is even simpler) Massimo
Edited By Massimo Dalmonte on 31/05/2019 07:35:33 |
| Martin Connelly | 31/05/2019 14:14:31 |
2549 forum posts 235 photos | I made a 127 tooth gear using the calculate each position method as 360 x X/127 and a stepper motor with a close coupled harmonic gearbox. It required 88.8888 steps per degree, just under 252 steps per tooth. I decided that was going to be accurate enough for my needs. Martin C |
| Brian Oldford | 01/06/2019 09:11:30 |
686 forum posts 18 photos | Posted by Bazyle on 30/05/2019 18:10:34:
In practice the problem has quite a low boundary. You are only ever going to cut gears up to 200 (plus whatever the JW large wheel skeleton uses) so the number of variables is quite small. For each of those 200 you need a maximum of 200 entries, average 100, in a table telling you how many steps to take. So the memory requirement is only 200x100 off 16bit numbers. You can do the calculations in excel and blow them into an eprom (except nobody does that anymore) have a few switches on the high address lines to select the tooth count and a couple of counters take the values and do the steps. No processors needed ! Whilst seemingly a very elegant solution for its simplicity , For "awkward" divisions won't that encounter the problem of cumulative error mentioned upthread? |
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - Winter Storage Of Locomotives
04/10/2023 21:02:11 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!










 Register
Register Log-in
Log-in


