Old School Drawing Exercises and 2D CAD
| SillyOldDuffer | 03/07/2020 12:23:07 |
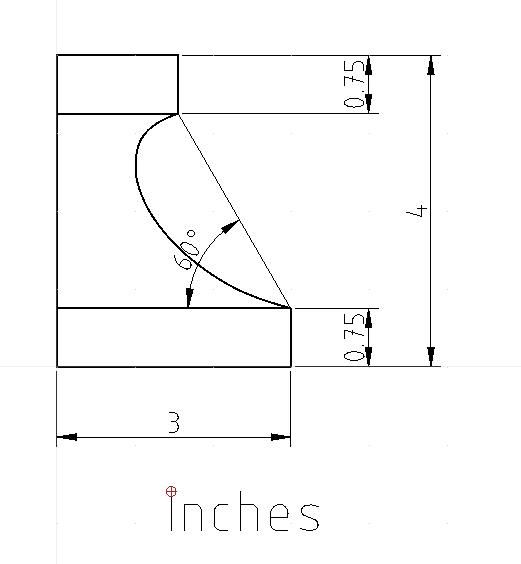
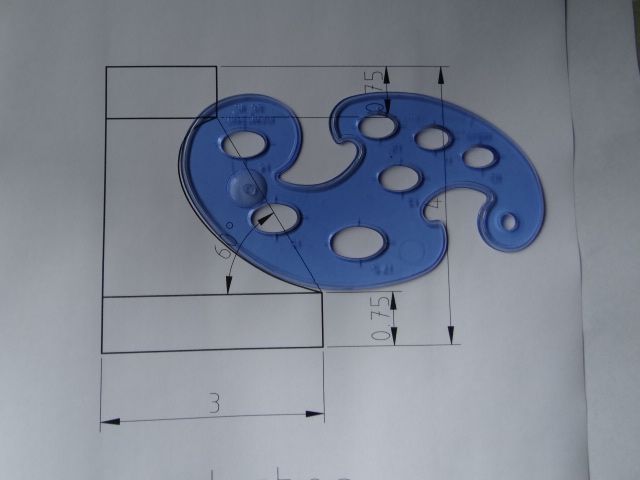
| 10668 forum posts 2415 photos | While I ponder Michael's problem and worry from his video if Thales is pronounced Thay Lees or Talez, here's another hard one. Well I think it's hard! Replicate the curve of this moulding by whatever method. Clue - it's generated from a 1.5" radius semicircle, but the semi-circle's origin isn't on the 60° line. Whilst a CAD package can draw the spline curve given relatively few points to follow, producing a 'fair curve' manually needs several.
Nigel complained about hard-to-make drawings and this might be a good example! But shapes like this are common in the real-world. Streamlining and decorative work demand tricky curves, and made cheaply too! My stair bannister is an example, and dining room coving is another. No sympathy for the poor old tool-maker - the curve has to look right! Dave
|
| Georgineer | 03/07/2020 12:26:27 |
| 652 forum posts 33 photos | This thread is taking some very interesting directions. Keep it up, lads! And Neil,your knurler looks useful. Would it make a suitable subject for MEW? George B. |
| Georgineer | 03/07/2020 12:29:23 |
| 652 forum posts 33 photos | SOD, when my wife worked for the engineering firm Thales it was pronounced Tallis! G.
|
| Neil Wyatt | 03/07/2020 12:56:48 |
19226 forum posts 749 photos 86 articles | Posted by SillyOldDuffer on 03/07/2020 12:23:07:
While I ponder Michael's problem and worry from his video if Thales is pronounced Thay Lees or Talez, here's another hard one. Well I think it's hard! Replicate the curve of this moulding by whatever method. Clue - it's generated from a 1.5" radius semicircle, but the semi-circle's origin isn't on the 60° line. Whilst a CAD package can draw the spline curve given relatively few points to follow, producing a 'fair curve' manually needs several.
Nigel complained about hard-to-make drawings and this might be a good example! But shapes like this are common in the real-world. Streamlining and decorative work demand tricky curves, and made cheaply too! My stair bannister is an example, and dining room coving is another. No sympathy for the poor old tool-maker - the curve has to look right! Dave
With CAD the curve is best done as a simple bezier with a control point at each end. Trivially simple. Manually just as easy using French curves, the hard bit being finding mine if they turn out not to be where I put them years ago... Neil |
| Neil Wyatt | 03/07/2020 12:57:44 |
19226 forum posts 749 photos 86 articles | Posted by Georgineer on 03/07/2020 12:26:27:
This thread is taking some very interesting directions. Keep it up, lads! And Neil,your knurler looks useful. Would it make a suitable subject for MEW? George B. It's not mine, it's Gary's! Not 100% sure but I think the design looks familar. Neil |
| duncan webster | 03/07/2020 12:59:51 |
| 5307 forum posts 83 photos | SODs latest: assuming we are to use 2 arcs, unless both radii are specified there are an infinite number of solutions |
| blowlamp | 03/07/2020 13:22:38 |
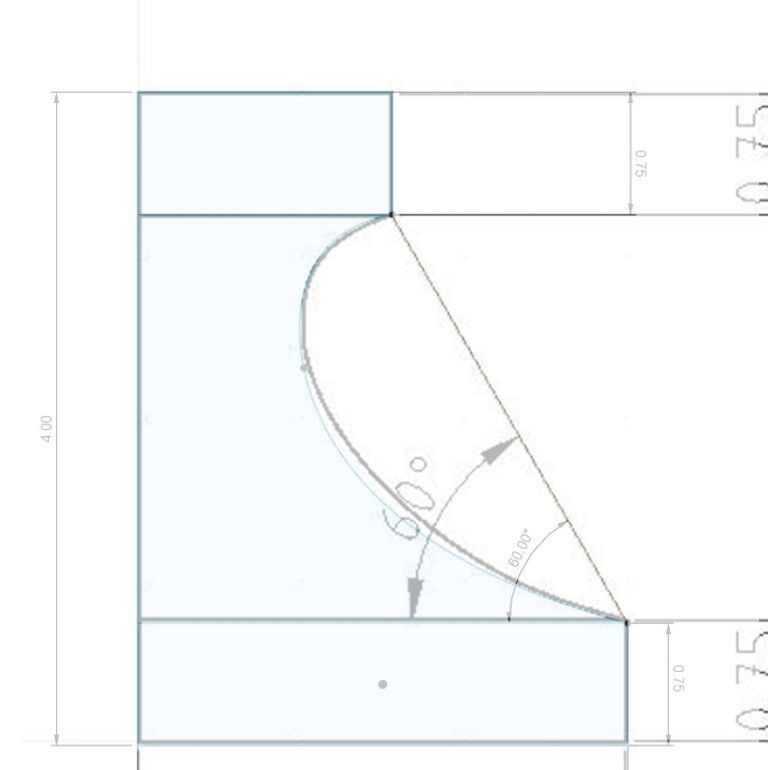
1885 forum posts 111 photos | My best guess for the centre location of the 1.5" rad arc is at about 2.5" to the right & 1.5" down from the top/left corner. I'm suspecting a 0.625" rad arc at the top and a 3.125" rad arc at the bottom to join all three together tangentially.
Martin. |
| Gary Wooding | 03/07/2020 13:45:41 |
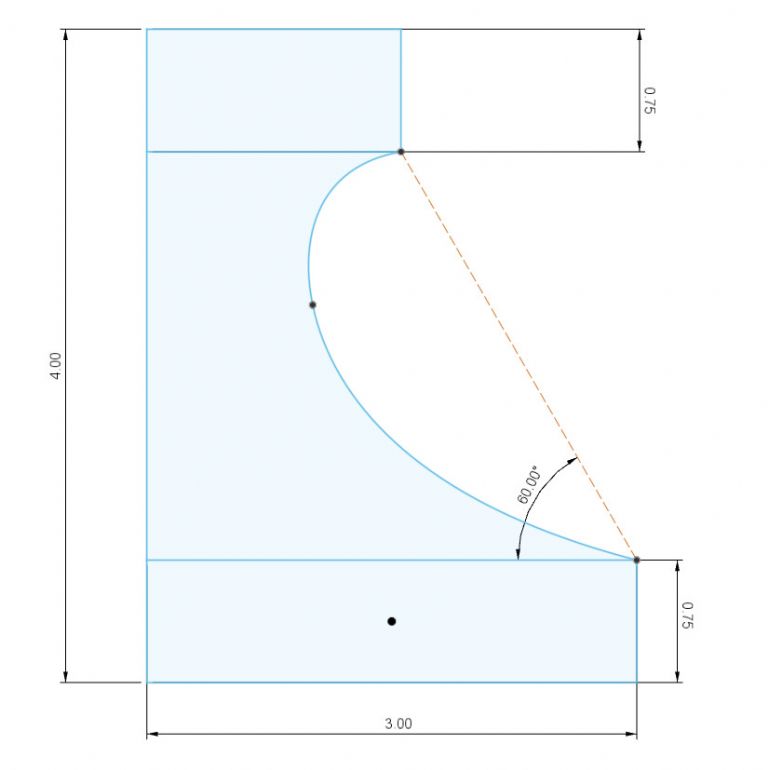
| 1074 forum posts 290 photos | How about this?
|
| Gary Wooding | 03/07/2020 13:54:44 |
| 1074 forum posts 290 photos | Posted by Neil Wyatt on 03/07/2020 12:57:44:
Posted by Georgineer on 03/07/2020 12:26:27:
This thread is taking some very interesting directions. Keep it up, lads! And Neil,your knurler looks useful. Would it make a suitable subject for MEW? George B. It's not mine, it's Gary's! Not 100% sure but I think the design looks familar. Neil It was published in issue 72 of MEW, called Yet Another Knurling Tool
|
| SillyOldDuffer | 03/07/2020 13:55:13 |
| 10668 forum posts 2415 photos | Posted by Neil Wyatt on 03/07/2020 12:56:48:
Posted by SillyOldDuffer on 03/07/2020 12:23:07: ...
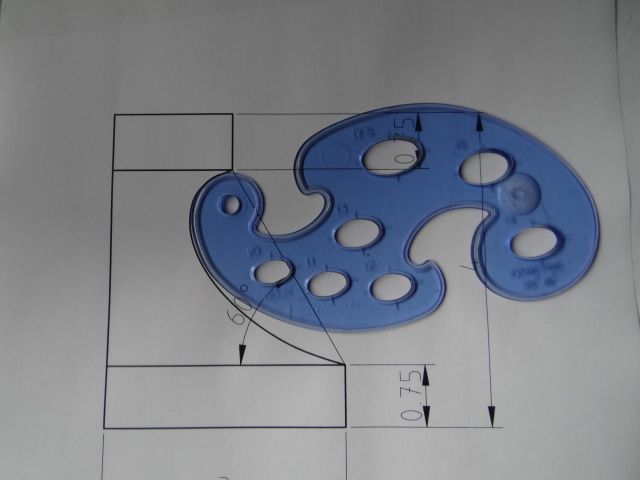
With CAD the curve is best done as a simple bezier with a control point at each end. Trivially simple. Manually just as easy using French curves, the hard bit being finding mine if they turn out not to be where I put them years ago... Neil CAD may make drawing Bezier curves easy thank goodness, but are they trivially simple? Doing this manually, I'd use a French curve at different angles to fair the curve, but it would be lucky to find an exact match. One of mine comes close, but not at both ends: And someone designed that French curve on a drawing board in the first place! How was it done? Re Duncan's comment, I'm afraid the curve isn't drawn with arcs. (Maybe it could be?) Once the approach is explained, easy enough to do manually, with Qcad, or with any other competent 2D CAD package. Not sure about FreeCAD & Fusion360's sketch tools for this particular job. They might not have the 2D primitives needed to construct the curve. (I haven't checked.) They can both do spline curves, but in this example it might be easier to construct the outline in 2D CAD and import the answer rather than sketch it. Dave
|
| Gary Wooding | 03/07/2020 14:10:01 |
| 1074 forum posts 290 photos | Posted by SillyOldDuffer on 03/07/2020 13:55:13:
Once the approach is explained, easy enough to do manually, with Qcad, or with any other competent 2D CAD package. Not sure about FreeCAD & Fusion360's sketch tools for this particular job. They might not have the 2D primitives needed to construct the curve. (I haven't checked.) They can both do spline curves, but in this example it might be easier to construct the outline in 2D CAD and import the answer rather than sketch it. Dave
My effort was done with Fusion sketch. What's wrong with it? |
| SillyOldDuffer | 03/07/2020 14:15:11 |
| 10668 forum posts 2415 photos |
Pretty close, your curve goes slightly deeper than mine: I'm not complaining! Fusion did better than I thought it would! Dave Edited By SillyOldDuffer on 03/07/2020 14:16:39 |
| Michael Gilligan | 03/07/2020 14:18:35 |
23121 forum posts 1360 photos | Posted by SillyOldDuffer on 03/07/2020 13:55:13:
And someone designed that French curve on a drawing board in the first place! How was it done? …
. Not sure ... but I think it is literally a spline curve, so created with a suitably springy flexible strip and some pins. MichaelG. |
| Martin Connelly | 03/07/2020 14:36:37 |
2549 forum posts 235 photos | To me it looks like the curve produced by rotating a circle 45 degrees in two planes. At 1.5 radius this would produce an oval 3 high 2.12 wide. Rotate this 45 degrees anticlockwise to produce the example given. Martin C |
| SillyOldDuffer | 03/07/2020 16:06:10 |
| 10668 forum posts 2415 photos | Posted by Neil Wyatt on 03/07/2020 11:57:51:
Posted by Michael Gilligan on 03/07/2020 11:33:39:
What remains of my brain is at risk of frying ... So can anyone help me, please ? Taking Dave’s triangle as an example: We know that
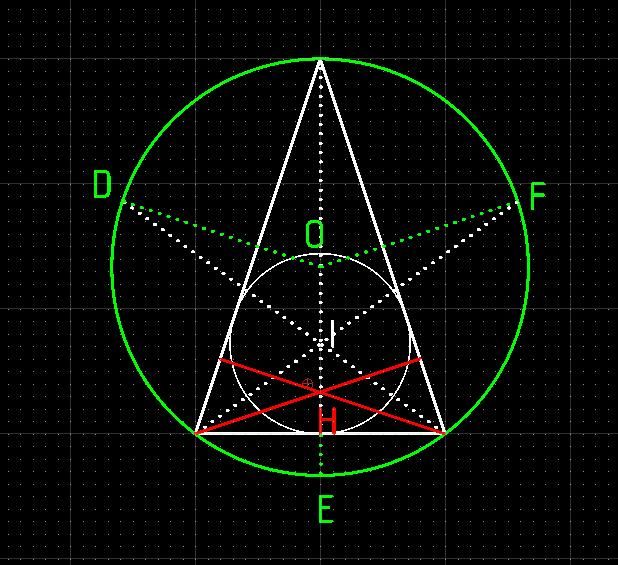
So ... There must be some elegant relationship between those two facts But what is it ? A geometric demonstration would be appreciated MichaelG. As a rider... There are actually THREE points defined solely by the triangle itself that all lie in a straight line. Michael has mentioned TWO, what is the THIRD? And what are their correct names (I had to look these up)? Neil Michael and Neil have caused a complete meltdown here. Now I know I know nowt about triangles! A guess; Neil means the centroid, incircle and orthocentre, all of which I had to look up and read four times. And there must be a million other triangle facts out there - my brain hurts. Anyway, noticed this coincidence not mentioned by Wikipedia's Triangle entry. The inner circle is located by bisecting the angles (point I), whereas the outer circle (point O) is located by dropping verticals from the centre of each side. The coincidence is the white bisectors and green mid-verticals meet together on the perimeter of the outer circle when they're carried on outside the triangle (Points D, E and F). More! The orthocentre is found by dropping the red verticals at a right angle into the triangle's opposite corner. They cross at the orthocentre (Point H). If the red and green lines are also carried across the circle, they too meet on the perimeter. So all three centres I, H and O are all related to each other, and Point H is also the triangle's centre of gravity. There's deep logic in this I don't understand. Arggh! Dave
|
| blowlamp | 03/07/2020 16:10:57 |
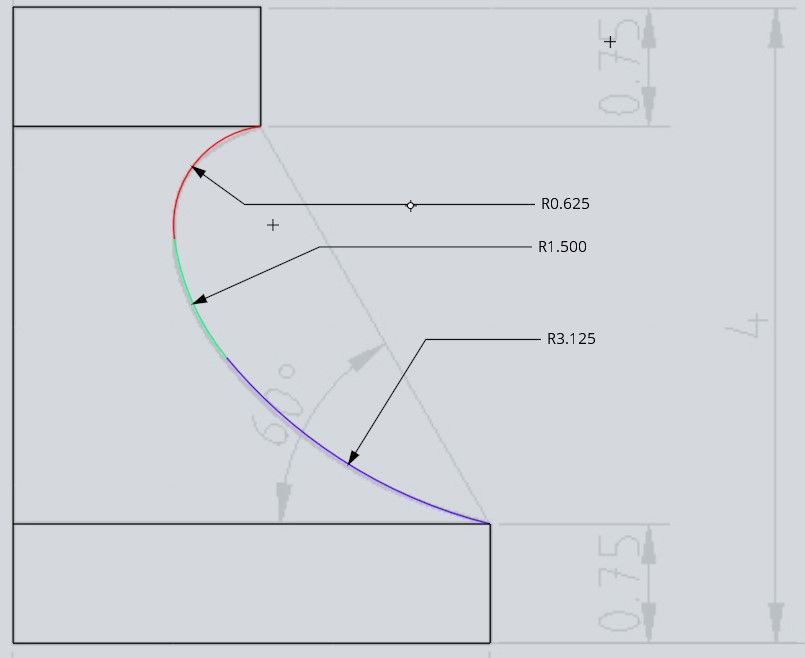
1885 forum posts 111 photos | Drawn with three arcs and it's not too far out, using SODs clue about the 1.5" arc.
Martin.
Edited By blowlamp on 03/07/2020 16:16:09 |
| pgk pgk | 03/07/2020 17:40:55 |
| 2661 forum posts 294 photos | Hang on.. this is a moulding so to replicate it you need the negative. Release agent and plaster may do the job..(ducks and runs..) pgk |
| Michael Gilligan | 03/07/2020 18:48:57 |
23121 forum posts 1360 photos | Posted by SillyOldDuffer on 03/07/2020 16:06:10: . Michael and Neil have caused a complete meltdown here. Now I know I know nowt about triangles! A guess; Neil means the centroid, incircle and orthocentre, all of which I had to look up and read four times. And there must be a million other triangle facts out there - my brain hurts. […] So all three centres I, H and O are all related to each other, and Point H is also the triangle's centre of gravity. There's deep logic in this I don't understand. Arggh! Dave
. I’m sure you’re on the [long] road towards understanding, Dave Sorry not to have participated ... I’ve been tinkering with microscopes, and leaving you to do all the work. MichaelG. . P.S. ___ Have you noticed that you are also, maybe, drawing a pentagram ? https://en.wikipedia.org/wiki/Pentagram Edited By Michael Gilligan on 03/07/2020 18:59:10 |
| duncan webster | 03/07/2020 19:19:04 |
| 5307 forum posts 83 photos | I'm still confused, the only constraints seem to be the 2 ends of the 60 degree construction line, and that fact that 1.5" radius comes into it somewhere. There are still an infinite number of solutions. |
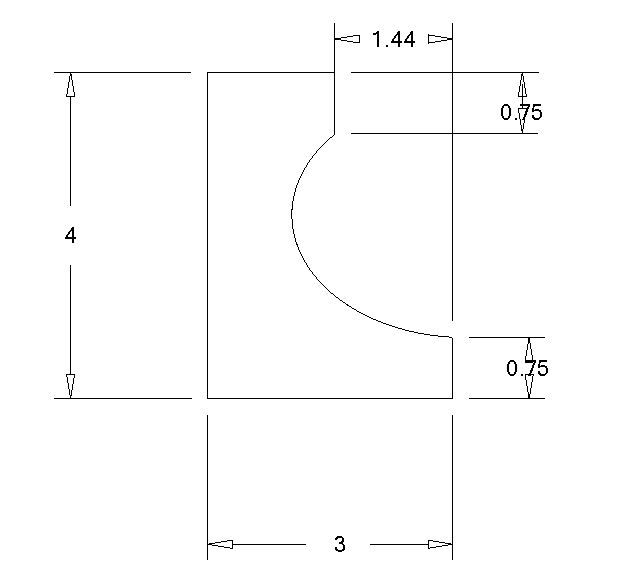
| JasonB | 03/07/2020 19:54:05 |
25215 forum posts 3105 photos 1 articles | How did I do? one line produced from a 1.5R semicircle
|
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - Winter Storage Of Locomotives
04/10/2023 21:02:11 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!

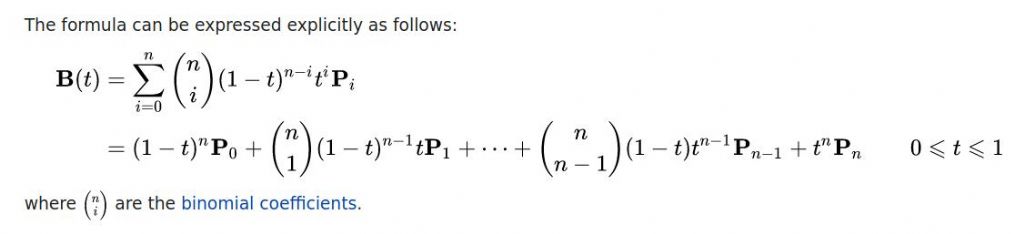









 Register
Register Log-in
Log-in


