3D graphing of mathematical functions
Introductory text needed please ...
| Frances IoM | 14/12/2016 21:44:01 |
| 1395 forum posts 30 photos | Michael - not knowing your technical background makes it difficult to suggest text books - also not knowing the basis of your interest - most of what you need is covered in the first year or so of an engineering degree (or the first couple of months of a maths degree assuming you have had a deeper grounding in Maths at sixth form level). As no doubt some have pointed out there is no royal road to maths - mathematicians tend to like rigorous development which technique has to be learnt before it becomes habitual (even tho it seems many mathematicians intuit a solution/theory and then prove it). You would I suspect be advised to get an engineering maths book published any time post WW2 which should cover the required calculus, fourier analysis etc - the basic maths will be found in textbooks dating from the late 1800s. |
| Michael Gilligan | 14/12/2016 22:04:44 |
23121 forum posts 1360 photos |
Posted by Michael Gilligan on 12/12/2016 21:49:37: . ... I don't want to just play about changing numbers. [infinite number of monkeys writing Shakespeare] So I started looking at simple stuff like spheres and cones ... and realised that I don't really 'have the basics' Ultimately, I'm interested in the way that natural shapes develop from simple expressions. [particularly, the forms of the Radiolaria] ... I have a copy of Turing's thesis on this; which I cannot understand, but I'm hoping that a more interactive graphics environment will help. I think it's what they call Lesson 1.01 that I need. . Frances, Thank for replying; but I think I answered your question in my opening post, and in my response to John ^^^.
I was hoping that in these enlightened times, there would be an interactive tutorial somewhere on the web, that started at a level which I could grasp without reading all those TextBooks and which would enable me to learn at my own pace; to the level that I need to reach to pursue my interest in the Radiolaria. Apparently not. MichaelG. . https://en.m.wikipedia.org/wiki/Radiolaria Edited By Michael Gilligan on 14/12/2016 22:06:29 |
| John Haine | 14/12/2016 23:11:11 |
| 5563 forum posts 322 photos | Michael, I can't do it now and I'm busy all tomorrow but I'll try and post an explanation of what I meant by "expect by looking at the function". Given you have this tool now, you can probably learn a lot by playing with it for various simple functions and slowly build up your knowledge. I'd guess that Open University maths texts should also be helpful as they can't assume A level as a starting point for example? |
| Michael Gilligan | 14/12/2016 23:15:41 |
23121 forum posts 1360 photos | Posted by John Haine on 14/12/2016 23:11:11:
Michael, I can't do it now and I'm busy all tomorrow but I'll try and post an explanation of what I meant by "expect by looking at the function". Given you have this tool now, you can probably learn a lot by playing with it for various simple functions and slowly build up your knowledge. I'd guess that Open University maths texts should also be helpful as they can't assume A level as a starting point for example? . That would be great, John ... Thank You ! Given a desire to learn; I think maybe I just need to get my toe in the door. MichaelG. |
| John Haine | 14/12/2016 23:16:42 |
| 5563 forum posts 322 photos | Michael, try this: |
| Michael Gilligan | 14/12/2016 23:17:53 |
23121 forum posts 1360 photos | Thanks again, John MichaelG. |
| John Haine | 16/12/2016 13:02:58 |
| 5563 forum posts 322 photos | Michael, OK, so your equation is this (slightly rewitten). The first thing is that the numbers, 0.75 / 5 / 5, don't really add anything. The 0.75 just scales the height of the fence to that value, and the 5's scale the values of x and y. A very common thing to do in maths in this sort of situation is to "normalise" the equation by removing scale factors if they can be restored easily if you want them but otherwise just clutter up the working. In this case we would just re-write the equation like this. So first I've scrubbed out the 0.75 as we can just multiply whatever value we get from the equation later by simple multiplication. Second I've removed the 5s (or actually the 25s as the 5s are squared) - if you wanted the result for particular values in the original formula you'd just multiply those values by 25 and insert the result in the second formula. It already looks simpler. Next it's written as "e to the minus()" as 1/anything is anything to the power -1. That isn't essential but looks tidier. You probably know that e is the so-called Euler's constant, or the base of natural logarithms. It's a bit like pi, turns up all over the place in maths. It equals 2.7182818284590452353602874713527....and goes on for ever. e to the power of something, or exp(something), gets very large very quickly as the something increases, it's exponential. So exp(1) = 2.717...; exp(2) = 7.389; exp(5) = 148.4...; exp(10) = 22,000.5; exp(25) = 72,004,899,337.4! As we have the reciprocal of the exponential in our formula, it gets very small very quickly. But also note that exp(0) = 1. So if x and / or y in our formula above were zero, the function is equal to one. x and / or y are zero along the top edges of the fence, so that's why the top is flat. Now imagine an ant exploring the surface carrying a tiny GPS that tells him his coordinates including height. Suppose that the y axis points North and the x axis points east. (And the earth is flat!) Now the ant crawls eastwards along a line of latitude "1" from say x=-5 to x=5. Along that line, since y equals 1, we could write the equation: At y=-5 the value of z is 1/72,004,899,337.4 = next to nothing! Since x is squared, z has the same value at x=+5. At x=+2 or -2, z is 0.018, so still pretty small. x=+/-1 gives z=0.37. You can see why we get the "fence" since the function gets very small very quickly. If the ant crawled along y=2, the function would be Since the value of the exponent is now 4 times larger, z is much smaller except when x is (if you like) 4 times closer to zero. This why the fence gets sharper as you get further from the origin. Incidentally, the function in the third equation is, except from some normalising factors, the same as the statistical "normal distribution" or "gaussian function". So the original function is a sort of two-dimensional gaussian (but in the real 2-d gaussian x squared and y squared are added not multiplied). I hope this explanation helps. Generally with most of the formulas you could apply similar technicques, by first getting rid of multiplying coefficients and then looking at the behaviour of the function if you keep one variable constant and vary the other, and do that for various "constant" values. In effect you will be producing cross-sections of the shape. The App should easily allow you to do that.
|
| SillyOldDuffer | 16/12/2016 13:21:50 |
| 10668 forum posts 2415 photos | Posted by John Haine on 16/12/2016 13:02:58:
Michael, OK, so your equation is this (slightly rewitten).
... In this case we would just re-write the equation like this.
...
John, Really good explanation but for us dumbos at the back would you please show step by step how you 'just' re-wrote the equation to get rid of the reciprocal? I know you got it right but I wasn't paying attention during that algebra lesson, and a good few others! Thanks, Dave |
| Russ B | 16/12/2016 13:29:58 |
| 635 forum posts 34 photos | Posted by Michael Gilligan on 13/12/2016 22:10:41:
Looking again at Ben Joffe's example [linked earlier], and qooted here: ... I think I am satisfied that my version is effectively the same. Apologies for the panic MichaelG. Still looking for that introductory tutorial. Is the colour a representation of the z value or have you/can you add a simple 4th dimension with this program? (ie. colour - I can't think of many other ways to add a simple 4th dimension) |
| Michael Gilligan | 16/12/2016 13:34:37 |
23121 forum posts 1360 photos | John, Very much appreciated ... I will work carefully through that [to make sure that I comprehend], before asking for more. I think [hope] that I can get to grips with things "this way round" ... But I foresee big problems coming if I have a particular shape in mind, and wish to write an equation that produces it. The App is amazing, and with your encouragement I'm confident that I will at least improve my understanding. MichaelG. |
| John Haine | 16/12/2016 14:15:41 |
| 5563 forum posts 322 photos | Posted by SillyOldDuffer on 16/12/2016 13:21:50:
Posted by John Haine on 16/12/2016 13:02:58:
Michael, OK, so your equation is this (slightly rewitten).
... In this case we would just re-write the equation like this.
...
John, Really good explanation but for us dumbos at the back would you please show step by step how you 'just' re-wrote the equation to get rid of the reciprocal? I know you got it right but I wasn't paying attention during that algebra lesson, and a good few others! Thanks, Dave Dave, I'm sorry I can't, offhand! It's just convention that one can write exp(-x) = 1/exp(x). If you plug some numbers into a calculator you'll find it always works. It can probably be proved but I have a suspicion it needs complex variables and logarithms to do so (or at least logs). |
| John Haine | 16/12/2016 14:18:17 |
| 5563 forum posts 322 photos | Posted by Michael Gilligan on 16/12/2016 13:34:37:...But I foresee big problems coming if I have a particular shape in mind, and wish to write an equation that produces it.
That is certainly true! If you really have to do that it's an "approximation" problem and usually it will only be an approximation. Sometimes if you want a shape to do something (a cam for example) it might be easier to see if you can use a shape you can mathematically generate rather than find an approximation. |
| SillyOldDuffer | 16/12/2016 14:27:30 |
| 10668 forum posts 2415 photos | Posted by John Haine on 16/12/2016 14:15:41:
Posted by SillyOldDuffer on 16/12/2016 13:21:50:
Posted by John Haine on 16/12/2016 13:02:58:
Michael, OK, so your equation is this (slightly rewitten).
... In this case we would just re-write the equation like this.
...
John, Really good explanation but for us dumbos at the back would you please show step by step how you 'just' re-wrote the equation to get rid of the reciprocal? I know you got it right but I wasn't paying attention during that algebra lesson, and a good few others! Thanks, Dave Dave, I'm sorry I can't, offhand! It's just convention that one can write exp(-x) = 1/exp(x). ... No problem John, I'll do some digging. I use conventions too, which is OK until I misremember one, or never learned it. If I find out I'll share the answer. Might do it now, I've spent the afternoon downloading software only to find out it's the wrong package. A small sherry and a little maths might cheer me up. Dave |
| Michael Gilligan | 16/12/2016 16:17:22 |
23121 forum posts 1360 photos | Posted by John Haine on 16/12/2016 14:18:17:
Posted by Michael Gilligan on 16/12/2016 13:34:37:...But I foresee big problems coming if I have a particular shape in mind, and wish to write an equation that produces it.
That is certainly true! If you really have to do that it's an "approximation" problem and usually it will only be an approximation. Sometimes if you want a shape to do something (a cam for example) it might be easier to see if you can use a shape you can mathematically generate rather than find an approximation. . John, It's more a matter of "wanting to" than "having to" ... as I mentioned earlier; the underlying motive for this exploration is that I want some understanding [or at least appreciation] of how biological forms develop, A couple of years ago, I studied an original print of Mrs Bury's book 'Figures of remarkable forms' **LINK** https://blogs.princeton.edu/graphicarts/2007/09/one_of_the_great_botanicals.html and I have been hooked ever since. Alan Turing's paper on morphogenesis would [probably] explain a lot, if only I could cope with the maths ... but Turing didn't have the luxury of an iPad and the QuickGraph App, so the diagrams are rather sparse. MichaelG. . Edit: for info. here is Turing's paper ... http://dna.caltech.edu/courses/cs191/paperscs191/turing.pdf Edited By Michael Gilligan on 16/12/2016 16:20:14 |
| John Haine | 16/12/2016 17:02:18 |
| 5563 forum posts 322 photos | Got it. where you lake the logarithm to base a. But the log of 1 to any base is zero, and the log to base a of a is 1. |
| Roger Head | 16/12/2016 23:52:29 |
| 209 forum posts 7 photos | Posted by SillyOldDuffer on 16/12/2016 13:21:50:
Posted by John Haine on 16/12/2016 13:02:58:...
In this case we would just re-write the equation like this. John, Really good explanation but for us dumbos at the back would you please show step by step how you 'just' re-wrote the equation to get rid of the reciprocal? I know you got it right but I wasn't paying attention during that algebra lesson, and a good few others! Thanks, Dave
Dave, it's just one of those things that flash past in a maths class - if you miss it, you're stricken forever-after. You can swap terms between numerator and denominator (or visa-versa) so long as you change the sign of the exponent. Another is the counter-intuitive "anything (number, expression, whatever) raised to the power of zero has a value of 1" Roger |
| Gary Wooding | 17/12/2016 10:57:02 |
| 1074 forum posts 290 photos | Hopefully, this might make exponents a little clearer... |
| SillyOldDuffer | 17/12/2016 18:33:39 |
| 10668 forum posts 2415 photos | Thanks guys. Where were you when I was doing homework? I was quite pleased with this 'show by example' as it's similar to Gary's more general approach I would never have thought of John's logs in a month of Sundays. If only I'd paid attention at school! Thanks, Dave |
| Michael Gilligan | 22/12/2016 23:04:12 |
23121 forum posts 1360 photos | I think I may have found my introductory text: **LINK** http://mathinsight.org/interactive_gallery_quadric_surfaces_introduction [One page in a very thoroughly hyperlinked collection of documents] The interactive examples are written in Java; so won't run on the iPad, but should be O.K. on the Mac. ... so; I can transcribe equations to QuickGraph on the iPad as I work through them Thanks again to John & Roger for the very helpful notes. MichaelG. |
| Rik Shaw | 23/12/2016 09:54:42 |
1494 forum posts 403 photos | z=z+z+z =zzz |
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- hemingway ball turner
04/07/2025 14:40:26 - *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!

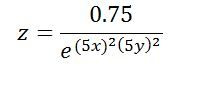
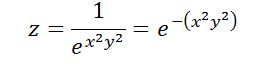
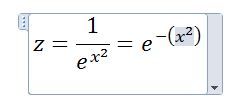
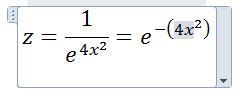

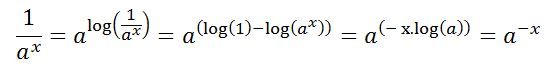

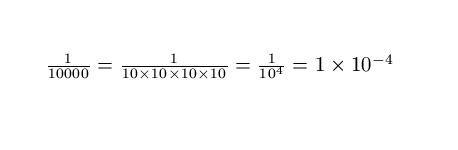









 Register
Register Log-in
Log-in


