Spacing of buttons for making involute cutters
| JOHN KNIGHT | 03/03/2014 18:20:27 |
| 15 forum posts | Gentelmen (and Ladies) I am about to try making a replacement gear (16DP 14.5deg PA 56 teeth) and need first to make a suitable cutter. I have read Ivan Laws book, and obtained an excel spread sheet giving sizes for the buttons and their spacing for 14.5 deg, from a kind Gent via the internet. However in a quest to actually understand what I am doing, I would like to know how the button cutter spacing and infeed is derived. I can work out the size of the button cutters, but the spacing and infeed have eluded me. Can anyone enlighten me please? Regards John |
| John Haine | 03/03/2014 18:32:21 |
| 5563 forum posts 322 photos | Look for the mikesworkshop site on Google, he has a page explaining the geometry which is very good. |
| IanT | 03/03/2014 18:32:58 |
| 2147 forum posts 222 photos | This is something I've haven't got around to yet John but I have gathered some information for when I do... There is some info that you may (or may not) have seen at 'Mike's Workshop' here: I'll quote the pre-amble "Making gears requires making a cutter with the appropriate profile. The amateur machinist usually does this using the button method developed by Ivan Law and further improved by John Stevenson. They have both given tables for the button diameter, button spacing and infeed required to produce the cutter. This method relies on the fact that the involute curve can be closely approximated to a circle over the limited distance of a gear tooth. I don't know if the John Stevenson referred to is the same one who moderates on here but if he is, then I'm sure he can provide better information on this than I can - but hopefully this will still be of use to you. Regards,
IanT |
| IanT | 03/03/2014 18:33:43 |
| 2147 forum posts 222 photos | Ooops - sorry John beat me to it! IanT |
| Brian Wood | 03/03/2014 19:02:58 |
| 2742 forum posts 39 photos | Hello John, John Haine beat me too, but Mike deals with Module calculations. On his making gear cutters pages, in the summary you will find useful formulae that equate button diameter, spacing and in feed in terms of number of teeth, the module (M) and pressure angle (p) Substitute M = 1/DP and you then have equations to help you directly. The tables at the bottom of that page are multipliers based on gear unit 1 Regards Brian Edited By Brian Wood on 03/03/2014 19:30:54 |
| Neil Wyatt | 03/03/2014 20:16:40 |
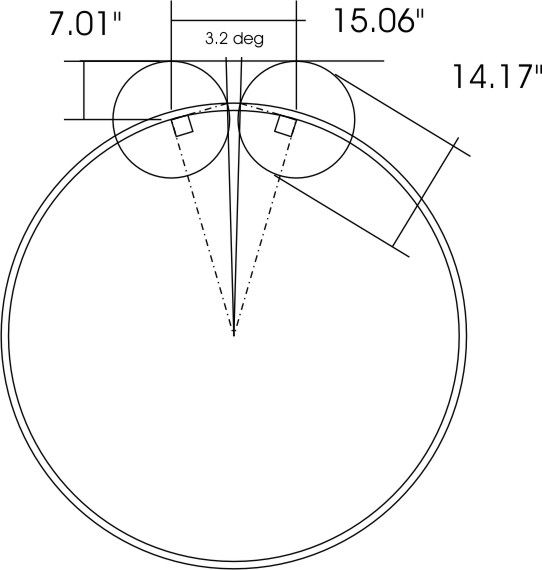
19226 forum posts 749 photos 86 articles | If you study figure 89 on page 113 of Ivan Law's book, it becomes apparent (after sufficient brain-wrangling) that the centre distance and infeed can be calculated by a certain amount of extra trignometry or by a graphical method (on paper or computer screen). Darn it, it's easier to do than describe -does this help? WARNING - INFEED DISTANCE IS WRONG - I SHOULD HAVE DRAWN AN INNER CIRCLE OF RADIUS 1/2pcd-DEDENDUM AND MEASURED FROM THAT! Otherwise this is correct for 14.5 degree 56 tooth gears at 1DP.
The basic distance between buttons is calculated from knowing the length of the arc between two opposing pitch points either side of a gap. The infeed is calculated along a line that bisects the arc between the pitch points. Much easier to draw than do the trig... just draw a pitch circle and base circle with four radii with angles between them of pitch angle, 180/number of teeth, pitch angle. Using fig89 as a guide draw the circles and measure off the diameter, spacing and infeed. I know this can be done, as against the odds, I made a 20-degree cutter for 13-tooth 20 DP gears. They needed very slight easing at the base of the tooth spaces, but other than that worked fine with other home made 20DP gears. For the record my figures were Cutter No 7.5 Teeth 13 D 4.50" C 5.65" E 2.25"
Neil
|
| Michael Cox 1 | 03/03/2014 22:14:30 |
| 555 forum posts 27 photos | Posted by Brian Wood on 03/03/2014 19:02:58:
Hello John, John Haine beat me too, but Mike deals with Module calculations. On his making gear cutters pages, in the summary you will find useful formulae that equate button diameter, spacing and in feed in terms of number of teeth, the module (M) and pressure angle (p) Substitute M = 1/DP and you then have equations to help you directly. The tables at the bottom of that page are multipliers based on gear unit 1 Regards Brian Edited By Brian Wood on 03/03/2014 19:30:54 I have a version of the spreadsheet which will work out the button diameters, spacing and infeed for both module and DP gears. Just contact me via the contact form on my website for a copy. http://mikesworkshop.weebly.com/ Mike |
| JOHN KNIGHT | 04/03/2014 07:49:09 |
| 15 forum posts | Thankyou to all who replied to my question. In less than 24 hrs I have the information from several sources. All I have to do now is make a cutter, then a gear. Regards John |
| John Stevenson | 04/03/2014 10:04:48 |
5068 forum posts 3 photos | John, Here's a simple and quick write up on cutting an involute spline which is really a stub gear to all intents and purposes.
It was written for the express purpose of doing a quick and dirty job, with the least equipment needed, but still do the job properly. It shows how to make the button cutter, how to make the actual cutter with relief which is what many don't show. This means it keeps it's shape thru numerous regrinds and finally the cutting of the shafts. |
| IanT | 04/03/2014 10:10:31 |
| 2147 forum posts 222 photos | I get the general idea Graham but I'm sure it's not quite that easy. I understand the basic principles of the button method but can you provide a bit more practical detail of what/how you are making the cutters shown here? (Sorry probably being a bit dense) I am in the process of designing/building a small electric locomotive and I'm thinking of powering all four axles (axle hung motors) so will probably need to build four 2-stage gearboxes for it. I could use commercial gears but it all mounts up cost-wise. I guess I will want something like 0.75 mod gears. If I'm only meshing with my own gears does that also ease the machining problems? Regards, IanT |
| John Stevenson | 04/03/2014 10:25:08 |
5068 forum posts 3 photos | Ian, Read the link I posted above. It gives a way to make cutters a lot simpler than Grahams [ but not as sexy |
| IanT | 04/03/2014 10:57:45 |
| 2147 forum posts 222 photos | I've just quickly read through John's link and it's very useful but the kind of topic that you really need to take some time to over to digest. I'll go over it again more slowly later. However, I did note that 'shaping' was mentioned (using a rack) and I was already aware of this option. I noted JS's response that most folk have a Mill (so will want to use that) but as I have both a Mill and a Shaper I have the luxury of choice. It really boils down to the time and effort involved and how much gear cutting is anticipated. My thinking (till now) was as follows; The fixture required for the Shaper will take quite a bit of time to make but (as I understand it) can be used with any gear Mod/DP size (within a reasonable range) and each 'rack' (or single point cutter) will then cut any gear within a Mod/DP size (so one cutter for 12, 33 & 60 tooth gears?). It is also a simple straight sided cutter, so not difficult to grind. The fixture might also be useful for other 'rotary' tasks on the shaper. Against this, the button method is good for making a single point cutter which only cuts one size of Mod/DP and I'd need at least two cutters to cut the two gear sizes I'm probably going to need for my loco. Any different gears needed and I'm back making new buttons and cutters again. So the button method may be quicker first time out but the shaper method may win long term if I'm going to do make more gears in different sizes. I hope this is a correct statement of the pro's & con's but please correct me if I've misunderstood anything. It is why I am interested in Grahams method as he mentioned it is quick to make a single point cutter, which is all I probably need for now and if I can skip the button making part, that might well swing it over anything other routes available to me. Regards, IanT |
| IanT | 04/03/2014 11:05:05 |
| 2147 forum posts 222 photos | Sorry John, it takes me a while to type this stuff in, so my posts often appear after others already have added more comments - which I haven't seen. I will read all this information again and try to see what is going to work best for me. I do understand that my needs (in terms of gear sizes) and my 'capabilities' (in terms of machinery) are probably not the norm but everyone here is probably different to some extent. Cost is an issue for me but so is time. I used to think that I had lots of time but now I know it is also finite!
Thank you for your help. Regards, IanT |
| IanT | 04/03/2014 16:42:13 |
| 2147 forum posts 222 photos | Graham, thank you for responding so quickly and taking the trouble to explain the method further. Again, I'll have to go away and let this idea 'sink in' for a bit but it certainly looks like something I could manage. My thanks to both of you Gentlemen for your good advice. Regards, IanT |
| Neil Wyatt | 05/03/2014 19:36:06 |
19226 forum posts 749 photos 86 articles | One frustration with Ivan Law's excellent little book is the lack of a formula for teh base circle dimensions. I'm sure Andrew Johnston won't mind me sharing this gem, which should make trignometric calculation of button sizes much easier: The diameter of the base circle is defined as the PCD times the cosine of the pressure angle. Neil |
| DC31k | 20/10/2021 09:00:33 |
| 1186 forum posts 11 photos | Resurrection of a 7-year old thread... I have just stumbled across the following, which provides a method of calculating button diameter and spacing that I had not seen before (the computing power just was not available to Ivan Law when he wrote his book). The paper itself is only 31 years old. https://www.geartechnology.com/articles/0990/Approximating_an_Involute_Tooth_Profile/ Direct link to the paper itself: https://www.geartechnology.com/issues/0990x/bilhardt.pdf If anyone wants to duplicate his computer program, there is a very elegant solution for fitting a circle to three points here: https://stackoverflow.com/questions/28910718/give-3-points-and-a-plot-circle |
| Michael Gilligan | 20/10/2021 09:18:27 |
23121 forum posts 1360 photos | Posted by DC31k on 20/10/2021 09:00:33:
Resurrection of a 7-year old thread... I have just stumbled across the following, […] . Thanks for that ^^^ … I will grab it whilst I can [*] MichaelG. . [*] __ I will just add, en passant, that the link posted by John Stevenson is currently returning this message: Invalid Page URL. If this is an error and the page should exist, please contact the system administrator and tell them how you got this message. |
| Dave S | 20/10/2021 09:58:15 |
| 433 forum posts 95 photos | The bbs has had a software update and a lot of content is no longer where it was, even assuming it still exists. The way back machine will probably be able to find it on John’s old site. IIRC it involved using a cone drill to make the cutter as it already had relief angle on it. there was also a method of offset turning to create relief behind a “circular” tool - it ends up looking quartic for those who remember the allegro Dave |
| John Haine | 20/10/2021 10:00:14 |
| 5563 forum posts 322 photos | A good find that, DC. I have tried a somewhat similar approach where one selects a starting point as given by "Mike's Workshop" method (which essentially matches the curvature of the involute at the pitch point), then perturbs the centre and radius of the circle by a small amount and evaluates the maximum error. If this is less than the last time, preserve the values and perturb again. Continue like this, possibly reducing the perturbation each time, until the error is less than a preset limit or no better solution can be found after a set number of iterations. Edited By John Haine on 20/10/2021 10:04:54 |
| Michael Gilligan | 20/10/2021 10:37:17 |
23121 forum posts 1360 photos | Posted by Dave S on 20/10/2021 09:58:15:
.
. Thanks, Dave … Yes, with the benefit of your comment, I do recall reading it at the time. [ and I also remember the Austin All-Agro ] MichaelG. Edited By Michael Gilligan on 20/10/2021 10:38:13 |
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - Winter Storage Of Locomotives
04/10/2023 21:02:11 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!










 Register
Register Log-in
Log-in


