3D graphing of mathematical functions
Introductory text needed please ...
| Michael Gilligan | 12/12/2016 20:59:58 |
23121 forum posts 1360 photos | I am exploring QuickGraph, a wonderful iOS App that plots rotatable 3D graphs of mathematical functions, and I now realise that my schooling barely touched the topic. I need to find a 'friendly' tutorial on the web, to teach me the basics of 3D functions. Can anyone advise, please ? MichaelG. Edited By Michael Gilligan on 12/12/2016 21:06:32 |
| John Haine | 12/12/2016 21:23:36 |
| 5563 forum posts 322 photos | It's a slippery slope Michael... with that app you could probably learn more than you could from most tutorials. What do you particularly want to know? you could get ensnared in stuff like partial differentials quite easily if you wanted to go that far. But I must have a look at that app, it looks cool. |
| Ady1 | 12/12/2016 21:26:23 |
6137 forum posts 893 photos | I need to find a 'friendly' tutorial on the web You'll be lucky if you do. Mathematics is like a gigantic pi**ing competion in complicated explanations gleefully practiced by middle class alien life forms This one for example is quite literally, and simply, the inverse of a lottery probability (ie 3 balls 56 to 1 etc) If you tried to edit this very simple explanation into that wiki, it would be deleted As mentioned, that program could tell you a lot more than any tutorial, and more simply too Edited By Ady1 on 12/12/2016 21:27:59 |
| Michael Gilligan | 12/12/2016 21:49:37 |
23121 forum posts 1360 photos | Posted by John Haine on 12/12/2016 21:23:36:
It's a slippery slope Michael... with that app you could probably learn more than you could from most tutorials. What do you particularly want to know? you could get ensnared in stuff like partial differentials quite easily if you wanted to go that far. But I must have a look at that app, it looks cool. . Here's a link to the App store, John **LINK** There's a good library of 2D and 3D functions included, but I don't want to just play about changing numbers. [infinite number of monkeys writing Shakespeare] So I started looking at simple stuff like spheres and cones ... and realised that I don't really 'have the basics' Ultimately, I'm interested in the way that natural shapes develop from simple expressions. [particularly, the forms of the Radiolaria] ... I have a copy of Turing's thesis on this; which I cannot understand, but I'm hoping that a more interactive graphics environment will help. I think it's what they call Lesson 1.01 that I need. MichaelG. |
| Jimmeh | 12/12/2016 21:52:57 |
27 forum posts 12 photos | Whenever I need something a bit mathsy I refer to MathWorld . Its helped me out a lot over the years, particularly with 3D geometry. I know it isn't tutorials per say but its a great resource and may help you to find functions of interest. Please use recreational maths responsibly. James Edited By Jimmeh on 12/12/2016 21:56:22 |
| Michael Gilligan | 12/12/2016 23:15:26 |
23121 forum posts 1360 photos | Thanks for the input, Gentlemen MichaelG. |
| Michael Gilligan | 12/12/2016 23:40:41 |
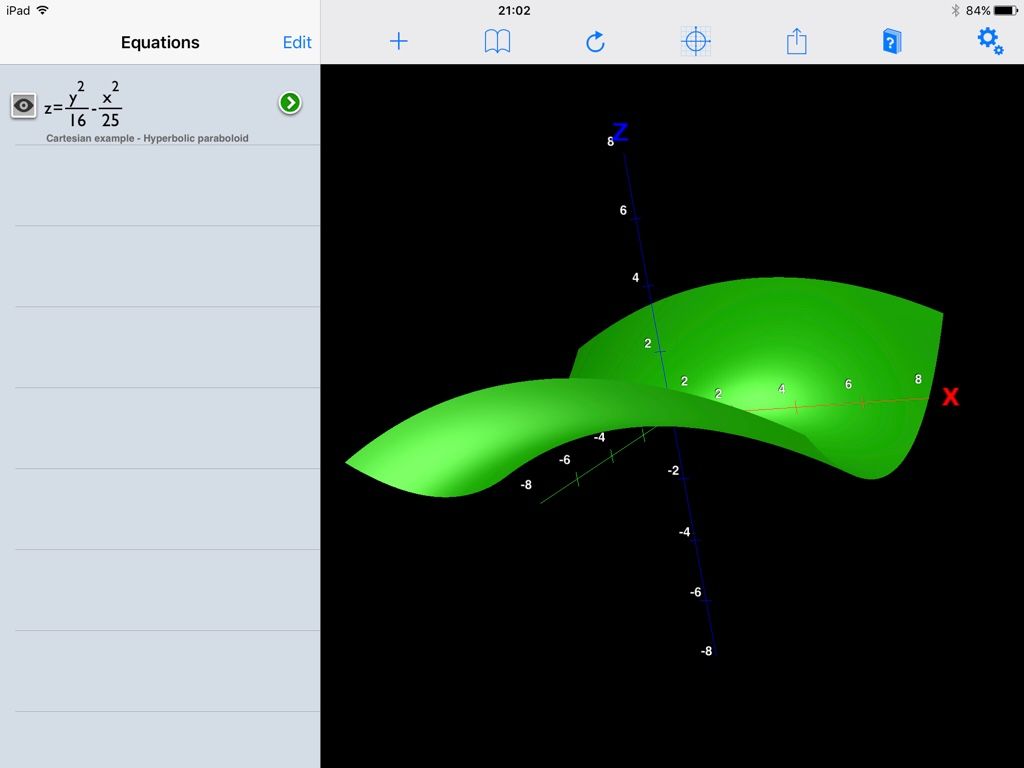
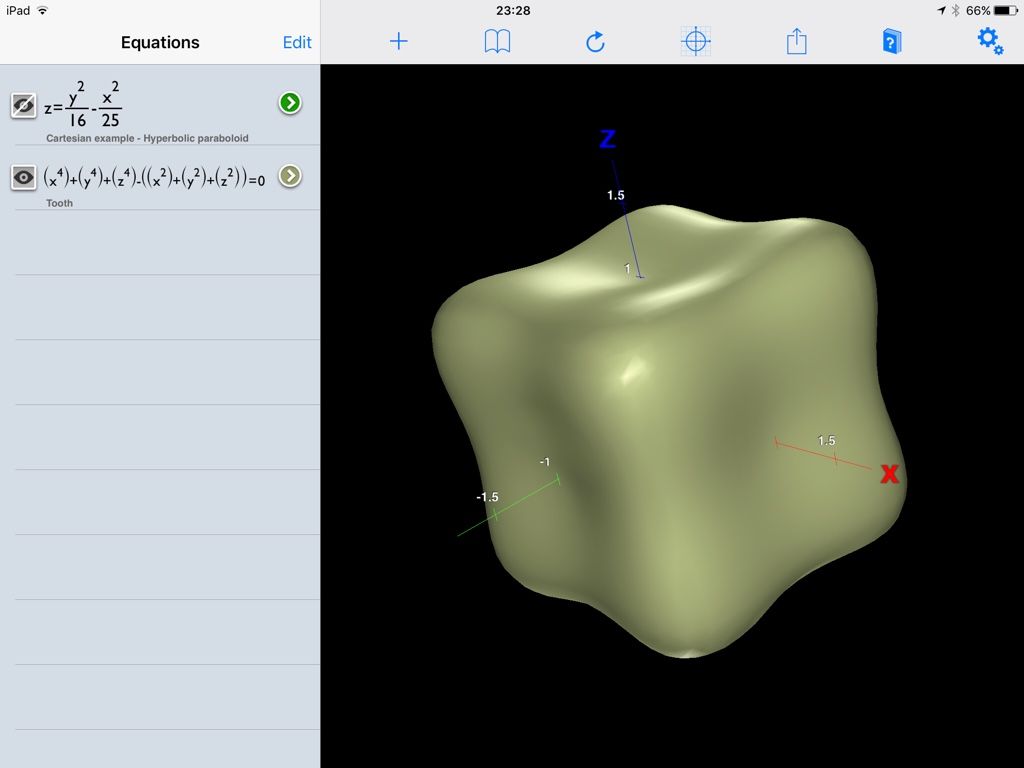
23121 forum posts 1360 photos | So ... Here is the Quartic Surface "Tooth" from James's 'Recreational' link: ... It works fine; but I'm 'Painting by Numbers' without any real understanding. I guess the next step is just to follow the Wolfram hyperlinks back from there, until I find my level. MichaelG. |
| Enough! | 13/12/2016 00:51:11 |
| 1719 forum posts 1 photos | Posted by Michael Gilligan on 12/12/2016 20:59:58:
I am exploring QuickGraph,
If you're into curves and such, you might enjoy the ios app "Harmonograph" for generating - unsurprisingly - harmonograph curves. It really is rather a good, and hypnotic, program. (Or you could go into the workshop and and build a mechanical version but the app is easier). |
| Neil Wyatt | 13/12/2016 08:06:32 |
19226 forum posts 749 photos 86 articles | Posted by Ady1 on 12/12/2016 21:26:23:
I need to find a 'friendly' tutorial on the web You'll be lucky if you do. Mathematics is like a gigantic pi**ing competion in complicated explanations gleefully practiced by middle class alien life forms This one for example is quite literally, and simply, the inverse of a lottery probability (ie 3 balls 56 to 1 etc) If you tried to edit this very simple explanation into that wiki, it would be deleted As mentioned, that program could tell you a lot more than any tutorial, and more simply too Edited By Ady1 on 12/12/2016 21:27:59 You are sadly right Ady, two areas of wikipedia are steadfastly defended by experts who rapidly expunge any 'plain English' explanation or interpretation: statistics and linguistics. The only way to try and understand them is to look up lots of arcane terms that are then explained in confusing ways and ultimately you end up going in circles.
|
| Michael Gilligan | 13/12/2016 08:36:14 |
23121 forum posts 1360 photos | Posted by Neil Wyatt on 13/12/2016 08:06:32: ... ultimately you end up going in circles. . ... and in 3D [sphere] there is an inflnity of circles to go round on.
|
| Michael Gilligan | 13/12/2016 09:57:24 |
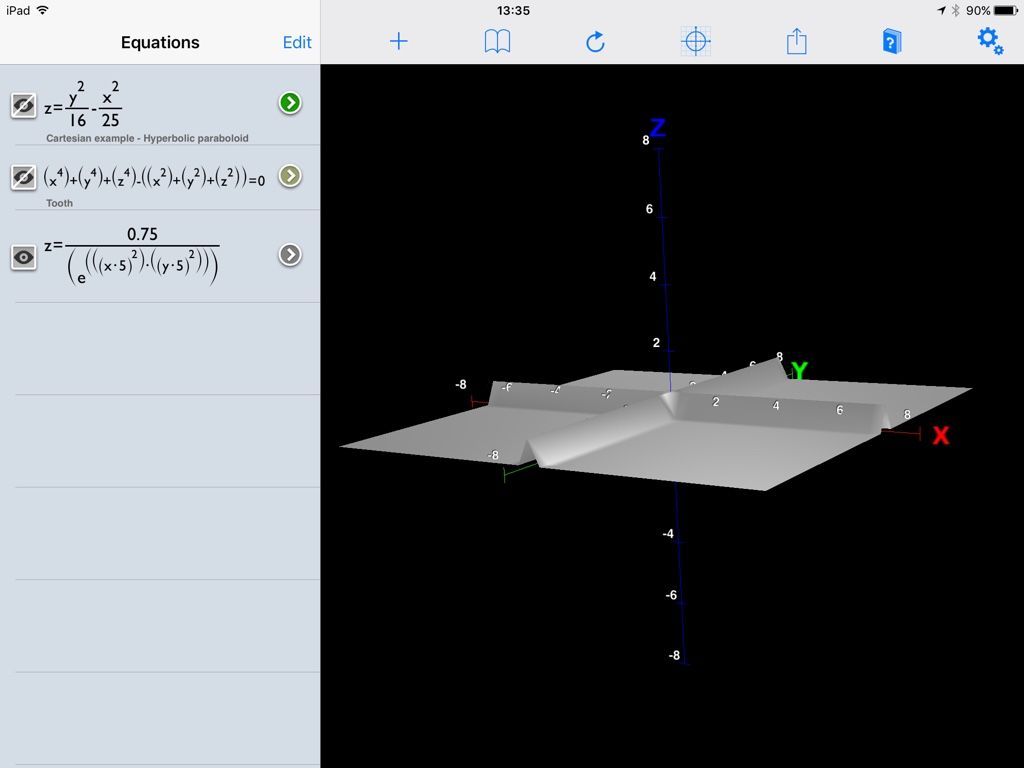
23121 forum posts 1360 photos | Perhaps I could try a specific question: This page **LINK** by 'benjoffe' has some interesting examples: https://www.benjoffe.com/code/tools/functions3d/examples The final item [intersecting fences] appeals to me ... but I haven't the foggiest idea how that function works, or even [since it is not shown as an equation] how to enter it into QuickGraph. So ... What do I do next ? MichaelG. Please don't answer with "Give-up, you're obviously not worthy" |
| John Haine | 13/12/2016 12:29:40 |
| 5563 forum posts 322 photos | Michael, he does give the equation: (z=) .75/[exp((x*5)^2*(y*5)^2] He doesn't give the z= bit at the start for any of his examples, and I assume that it is meant to have [brackets] as I have inserted. ? |
| Michael Gilligan | 13/12/2016 12:46:31 |
23121 forum posts 1360 photos | Thanks, John ... I will try that MichaelG. . As you will see ... I am struggling; because it is not obvious to me that his expression is 'inevitably' an equation to z Edited By Michael Gilligan on 13/12/2016 12:49:41 |
| Michael Gilligan | 13/12/2016 13:46:18 |
23121 forum posts 1360 photos | With John's advice, and the liberal application of parentheses ... I am nearly there with the 'intersecting fences' ... but mine look pointy, whereas the example by benjoffe has them curvy.
|
| Muzzer | 13/12/2016 14:26:02 |
2904 forum posts 448 photos | I suspect your axis scaling is simply different. He possibly has X and Y limits of +/- 2 or so. Possibly similar for Z? |
| John Haine | 13/12/2016 17:02:54 |
| 5563 forum posts 322 photos | You can see from the plot that the x and y limits are +/-7 in each case. The maximum value of the function is when either of both of x and y are zero, when the denominator is exp(zero) which is unity, so the max value is just the denominator, that is 0.75. I can't see from the picture here Michael. but as x or y get very big do the fences get very thin though their height remains the same? |
| Michael Gilligan | 13/12/2016 18:03:13 |
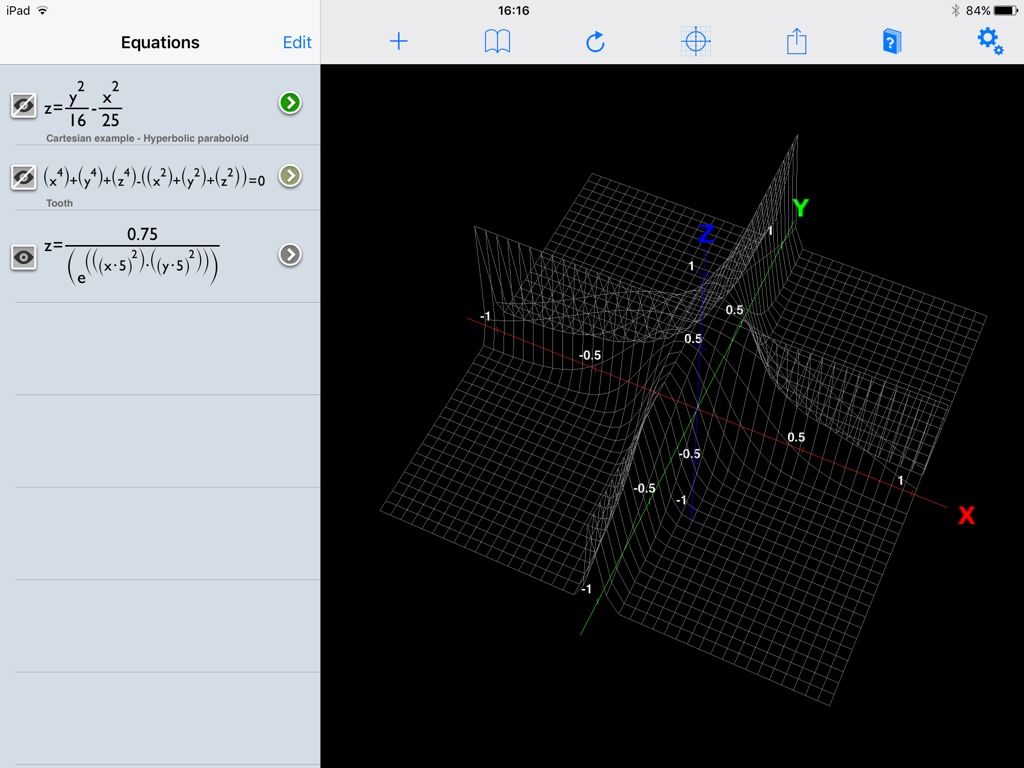
23121 forum posts 1360 photos | Thanks Muzzer & John, This is the same plot, as a mesh, and zoomed-in: . It is now evident, I think, that the problem is that the 'digital resolution' of the samples is rather coarse The App seems to default to +/- 8 on each axis, and re-scale when 'pinch-zoomed' ... but the resolution is not really sufficient to do justice to this particular function. ... Does that make sense ? MichaelG. |
| Michael Gilligan | 13/12/2016 22:10:41 |
23121 forum posts 1360 photos | Looking again at Ben Joffe's example [linked earlier], and qooted here: ... I think I am satisfied that my version is effectively the same. Apologies for the panic MichaelG. Still looking for that introductory tutorial. |
| John Haine | 14/12/2016 15:54:56 |
| 5563 forum posts 322 photos | I think you can see from this "zoomed in" view that the fences get sharper as x or y increase, which is kind of what you'd expect when you look at the function. |
| Michael Gilligan | 14/12/2016 16:43:30 |
23121 forum posts 1360 photos | Posted by John Haine on 14/12/2016 15:54:56:
I think you can see from this "zoomed in" view that the fences get sharper as x or y increase, which is kind of what you'd expect when you look at the function. . "... which is kind of what you'd expect when you look at the function."
I have very little intuitive undestanding of what that function would look like, and [perhaps more relevant to my interests] I wouldn't have the slightest idea where to start if I wanted to create a formula to produce that shape. MichaelG. |
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - Winter Storage Of Locomotives
04/10/2023 21:02:11 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!











 Register
Register Log-in
Log-in


