Old School Drawing Exercises and 2D CAD

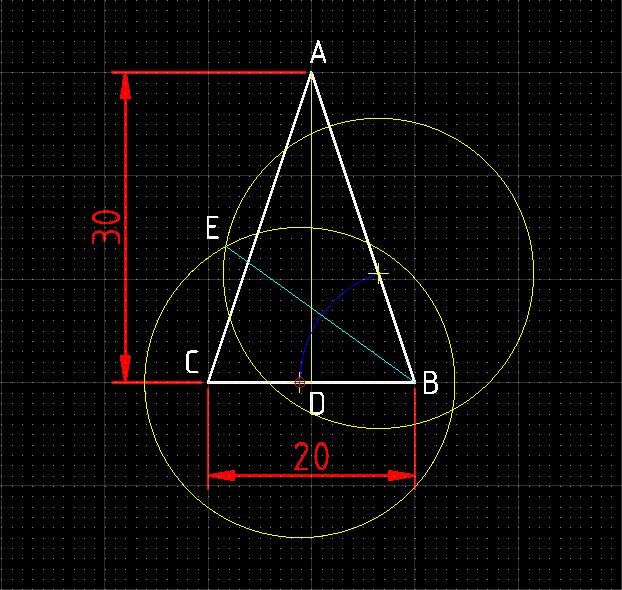
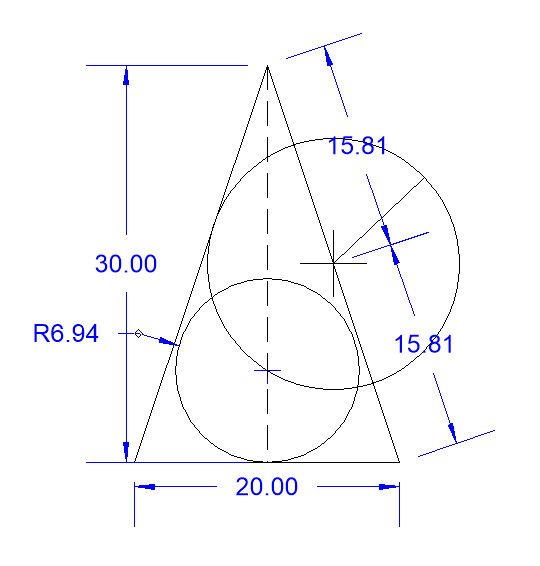
Apologies for complicating the circle in a triangle question by allowing folk to assume they had to draw the triangle itself with only a compass! No, it's the radius of the circle I was after - 7.207592

Gold star to Gary for solving it with trigonometry, but I have to mention he's used maths tools provided by someone else! Was it a calculator or a set of trig tables that delivered 71.565° ?

Some lessons learned:

1. The key to solving the problem is bisecting an angle, with luck this is remembered from school!
2. Need to know how to bisect an angle with a compass, or
3. Understanding a 2D CAD package will almost certainly have a tool for bisecting angles, in which case there's no need to remember points 1 & 2 above. CAD wins because it's quick and doesn't make mistakes, but the operator has to know which button to press! Beware of easy to use arty drawing software - it may not do techy stuff like this.

Can the entire problem be done with just a compass? Someone did in the distant past. Imagine a flat damp sand beach, a few sticks, a home-made compass and a length of string. The corners of the triangle can be found with the compass and fixed with sticks. A straight line can be marked on the sand by pulling the string tight between two sticks and twanging it on to the ground. Builders use much the same trick with chalky string to this day. No need for a hinged pair of compasses either - the 'compass' can be two sticks with a length of string held taut between them.

Here's bisecting done with a compass:

Steps:

1. Drop the vertical line AD
2. Draw an arc from the corner ABC that crosses AD (in Blue on Diagram)
3. Draw two circles from the each end of the blue arc where it meets AB and BC (Yellow on Diagram)
4. Draw a line from B to the intersection of the yellow circles. (Light Blue on diagram) This line bisects the angle ABC, and where it crosses AD is the centre of the biggest circle that will fit inside the triangle.

Comment - problem looks easy, but has hidden depths! More to technical drawing than CAD buttons or pencil and paper, but CAD hides a lot of underlying complexity.

Dave

Edited By SillyOldDuffer on 02/07/2020 12:33:57

That's sneaky, stating that a ruler could be used, after posing the question. The answer was simple in Turbocad, but I could not work out how to measure a 14.42 diameter circle with a compass.

Pete

[This posting has been removed]

Sorry Barrie,

I don't see how that works.

I tried it in CAD and the final circle, whilst tangent to the base, doesn't touch the other two sides.

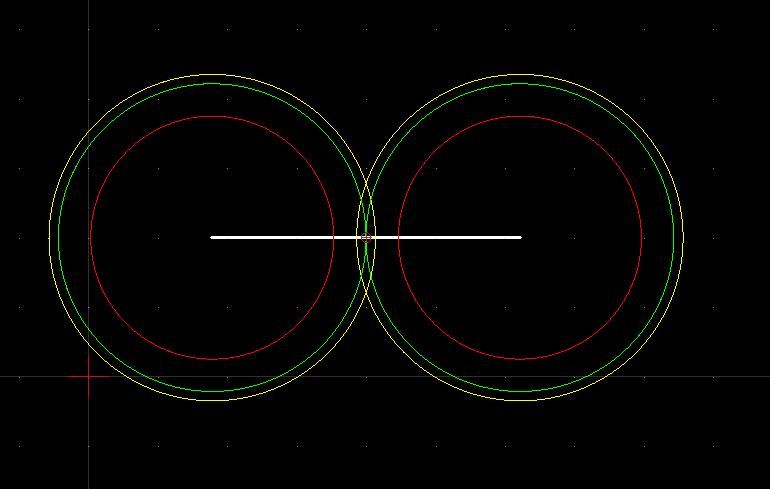
Yeah, sorry about that! My bad entirely - I'm in the dog-house again!

Going back to first principles again, a compass can determine linear distance by using it as a divider or a doubler. Quite easy to halve a line by setting a compass until the intersections it draws match exactly, and dividing can be repeated until the human eye can't cope.

The two red circles are obviously too small, and the two yellow circles equally obviously overlap. The two green circles are either spot on or pretty close.

Good eyesight can divide an inch down to 1/128ths, and dividing from another line at an angle to the target amplifies results allowing even finer graduations. Most struggle to read a 1/64" scale in practice. These days 1/32" is as good as this poor old duffer can do without a magnifying glass.

Dividing scales by factors of two is useful, but decimal scales are even better. Another drawing challenge is how to divide by 5 with a compass to make a decimal scale, and then a vernier? At this rate, engraving micrometers tomorrow!

Dave

That seems a bit complicated to me SoD.

I'd just draw two circles the same (but overlapping) size and then draw a line between their intersection points. That would give me the exact mid-point I'm sure.

IanT

Edited By IanT on 02/07/2020 14:49:48

[This posting has been removed]

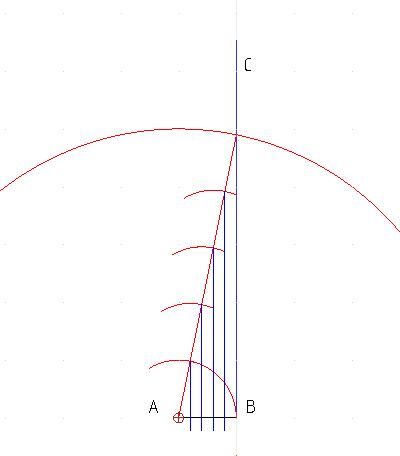
SOD's divide by 5 problem:

Draw a horizontal line AB 1 unit long. Erect a perpendicular from the right hand B.

Draw another line 5 units long by repeatedly stepping your compass. The set the compass to the length of this new line (5 units). Stick the point into A and swing an arc crossing the perpendicular through B at point C.

Then reset your compass to AB ( 1 unit) and mark off the diagonal line into 5 sections. Drop a perpendicular from each of these new points to AB and you've done it.

All sounds a bit long winded, but it can be a useful way of making an odd scale ruler.

Edited By duncan webster on 02/07/2020 14:53:24

You're right Ian, easier to do AND it would be more accurate!

Meanwhile, following Duncan's divide by 5 instructions:

You chaps are all too good at this...

Dave

Ah, but that needs a set square, ruler and pencil in addition to the compasses. Is that allowed now?

Pete

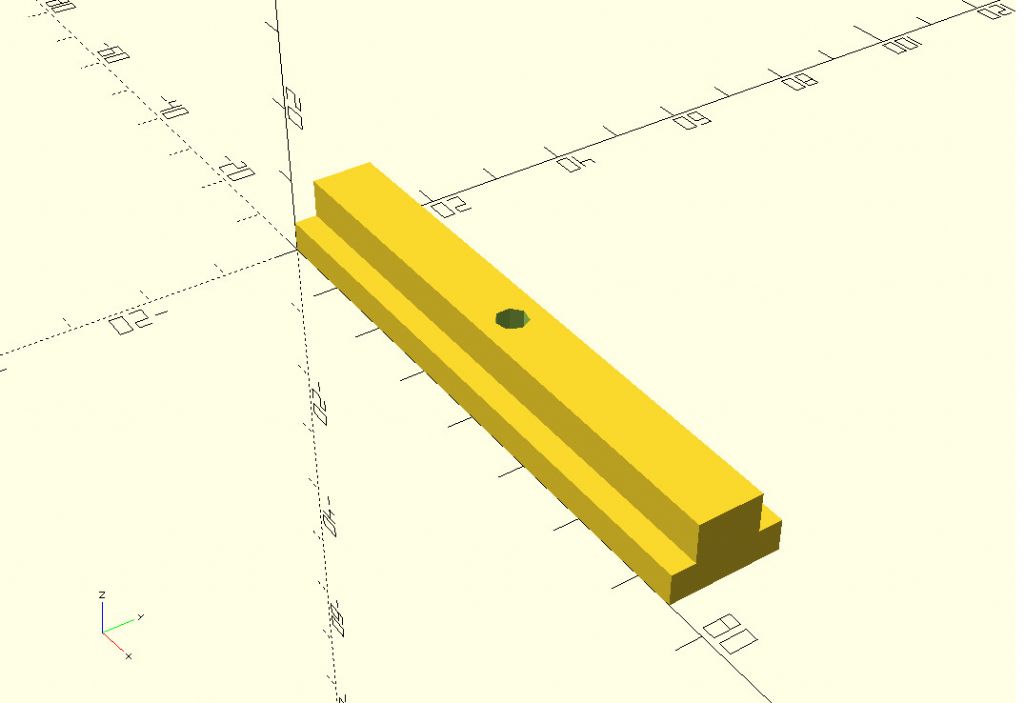
It's a rainy day outside (at least that's my excuse) so I've been amusing myself with Open SCAD.

There was a post recently about 3D printed T-Slot fillers. A nice simple thing to draw in 3D CAD (just sketch & extrude he says with new found confidence) but I thought I'd do it in SCAD (a much better use of coffee-time than Suduko!  )

Here is the script:

//
//
// T-Slot Filler - IanT
//
L = 75; // T-Slot Length
HR = 2; // Hole Radius
BW = 14; // Bottom (of Slot) Width
TW = 8; // Top (of Slot) Width
BH = 4; // Bottom (of Slot) Height
TH = 9; // Top (of Slot) Height
//
//
difference () {
union () {
cube ([L,BW,BH], center=false);
translate ([0,(BW/2-TW/2),0])
cube ([L,TW,TH]); }
translate ([L/2,BW/2,0])
cylinder (TH,HR,HR);
}

I've used arbitrary dimensions above, so just change the variables to what you need. I've not printed this myself (I think it might actually be quicker to just cut some wooden strips and glue them together?) but it should be fine.

You'll need to download Open SCAD and then just cut and paste the 'script' above into the Editor. For anyone not wanting to go "full-on" 3D CAD - Open SCAD can be learned in small steps and is pretty simple once you've got a few basics (it looks more complicated than it is) - and it also helps keep the little grey cells ticking over.

Regards,

IanT

Edited By IanT on 02/07/2020 17:18:16

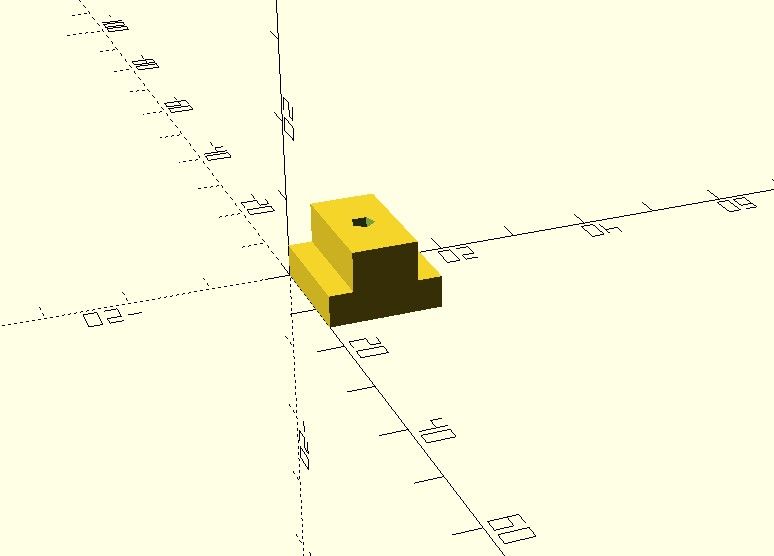
It also occurred to me that a printed T-Nut might be useful for holding things in place (where no or low loads were involved) - such as DTI mounts etc...

I just changed the length to 15mm and hole radius to 1.5mm (but would use tapping size in practice)

Regards,

IanT

.

With respect, Dave ... Your Step 1 is cheating, and disqualifies you.

But it’s simply a matter of adding the ‘mirror equivalent‘ of Steps 2&3 to locate the centre point.

... This also provides a legitimate way of placing that vertical, by construction.

MichaelG.

Edited By Michael Gilligan on 03/07/2020 00:15:36

That SCAD code looks rather like something someone at work once gave me, called POV-Ray.

Now, POV-Ray makes no pretence to be a CAD programme. It is or was intended to be purely artistic, and you can make it produce the most wonderful renderings of very pretty but utterly unfeasible or useless objects!.

It too uses command-lines that are fairly simple to grasp and somewhat similar to that SCAD example; and although engineering-drawing is not its intended purpose I wonder if in fact it, or an up-to-date edition, could be used for making 3D-printer files.

Something POV-Ray , or at least the version I have, lacks, are a grid or ruler-set, but I suspect you could make it generate at least a grid for the individual project.

To Pete, anything goes in my workshop. All's fair in Love, War and Model Engineering. Triple points for innovative cheating in my book, but don't try it in an Exam!

To Michael, no need for the 'with respect' - like Ian's comment on dividing, you are completely orthogonal...

Dave

.

The respect is genuine, Dave

You have provided another thought-provoking exercise to keep the little grey cells active.

MichaelG.

.

... upon which subject ^^^, allow me to throw this into the pot **LINK**

https://youtu.be/V5jQI8V3nsM

It’s a very nice proof of Thales’ Theorem

MichaelG.

What remains of my brain is at risk of frying ... So can anyone help me, please ?

Taking Dave’s triangle as an example:

We know that

1. the centre of the inscribed circle is located at the intersection of the ‘bisectors’ of the three angles
2. the centre of the circumscribed circle is located at the intersection the ‘perpendicular bisectors’ of the three sides

So ... There must be some elegant relationship between those two facts

But what is it ?

A geometric demonstration would be appreciated

MichaelG.

As a rider...

There are actually THREE points defined solely by the triangle itself that all lie in a straight line.

Michael has mentioned TWO, what is the THIRD?

And what are their correct names (I had to look these up)?

Neil

An excellent example, one great thing about 3D printing is the ability to incorporate clips and hinges.

Neil