Constrained Pendulum and Earth Rotation
| JA | 06/02/2017 19:24:23 |
1605 forum posts 83 photos | When I used "w" I meant the time period. I have yet to find the correct Greek letter on my keyboard or as a symbol for use in this script. I wish I had not entered this thread. Re-reading my first posting I realise that a simple pendulum clock will happily work at the poles. However there will be a very very small twisting force on the suspension. I think I will leave this thread to others and joining those students who ignored the conservation of angular moment. You cannot ignore angular momentum. JA Edited By JA on 06/02/2017 19:27:01 |
| Martin Kyte | 07/02/2017 09:53:23 |
3445 forum posts 62 photos | I did not understand the Foucault pendulum initially. Now I think I am clearer. My contention now is that the apparent motion at the pole is just the rotation of the earth, the plane of oscillation does not rotate and there is no coupling between the pendulum and the bob at this position. At the equator the pendulum and the earth are fully coupled and there is no differential rotation between the earth and the plane of oscillation (irrespective of its initial orientation) The rotating suspension couples into the bob.The pendulum rotates with the earth. The change of sign of apparent rotation moving the pendulum from the North to the South hemisphere is just the inversion of the pendulum with respect to North. I would be grateful for comments on the following statements. Best regards Martin Do say if you are fed up yet. |
| John Haine | 07/02/2017 09:55:58 |
| 5563 forum posts 322 photos | Imagine that the clock is fixed at the centre of a spinning wheel, turning at 1 rev per day, so that the pendulum vertical plane is perpendicular to the wheel. Further assume that the pendulum is replaced by a rotor that is spinning at some rate with the same rotational axis. This forms a gyroscope which is being rotated around an axis orthogonal to its spin axis, which generates a torque around the other mutually orthogonal axis. So that torque can have no effect on the spin speed of the gyro. Now assume that the flywheel is spinning against a spiral spring, so this becomes a balance wheel. Though its angular momentum keeps changing as energy is exchanged with the spring, the same argument applies at any instant. Now remove most of the rim of the wheel and replace the spring with gravity. It still looks the same. So there is no effect on the timekeeping of a pendulum constrained to swing in a plane, at least if located at a pole. |
| Martin Kyte | 07/02/2017 10:48:52 |
3445 forum posts 62 photos | I don't think that models it John. A pendulum swinging back a forth is a special case of a conical pendulum where the bob moves in a circle. The rotational axis is vertical. The bob motion can be represented as a sinusoidal and cosinusoidal. Reduce the amplitude of one of the components to zero and you have a pendulum swinging in a plane. I think you are absolutely right in the balance wheel statement that rotation in the same plane as the balance wheel will not affect the rate as the wheel will track with the escapement. I think this gyroscopic precession is what made Harrison move from vertical opposed oscillating bars to a horizontal balance wheel. The turning and corkscrewing of ships causing errors. regards Martin |
| John Haine | 07/02/2017 11:14:24 |
| 5563 forum posts 322 photos | Your original posting said that it was constrained to swing in one plane, not like a conical pendulum. That's the example I'm considering. If it can swing in 2 planes it's a Foucault pendulum. |
| Martin Kyte | 07/02/2017 11:36:42 |
3445 forum posts 62 photos | Hi John You are correct regarding constraint. I am just querying your assumed rotational axis. I think it is perpendicular to your spinning wheel ie is coaxial with the wheel's rotational axis. This I understand to be at right angles to your assumed rotational axis. Correct me if I am wrong. I quoted the conical pendulum to identify the rotational axis which does not change when only swinging in a plane. I think you model could be a good one I'm just not sure you are right about the axis which would lead you erroneous conclusions. However I am not clear I have really understood what you mean. Word diagrams are often difficult to interpret correctly. regards Martin |
| John Haine | 07/02/2017 11:52:45 |
| 5563 forum posts 322 photos | Not at all. It's just like the pendulum, the wheel's axis is horizontal, parallel to and fixed w.r.t. the plane. The plane is rotating aroud a vertical axis through the centre of the wheel, but perpendicular to the rotation axis. I'll try to produce a picture. |
| Martin Kyte | 07/02/2017 11:56:58 |
3445 forum posts 62 photos | Yes, but the the pendulums rotational axis is vertical through the suspension point. Martin |
| Geoff Theasby | 07/02/2017 12:00:59 |
| 615 forum posts 21 photos | I discovered the Coriolis effect as a child, playing on a roundabout. Trying to kick the central pillar whilst facing inwards, my foot was deflected to the left. In John Haine's posting just above, consider a small scaffold on a record turntable. A ball bearing suspended above the centre is set swinging. Now start the turntable and watch. Geoff |
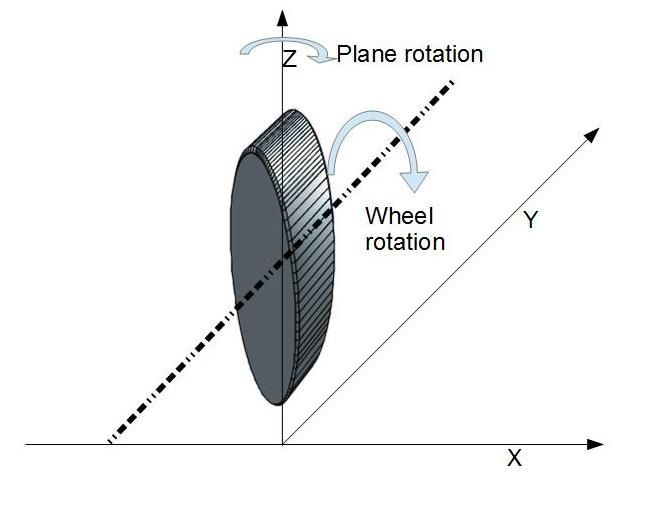
| John Haine | 07/02/2017 12:16:52 |
| 5563 forum posts 322 photos | This is what I mean.
The plane is XY (which could be the earth's surface near to the pole). The vertical axis is Z, and the plane rotates around Z. The wheel axis in this case is horizontal and parallel to the Y axis. The wheel rotates around this. The vertical axis through the wheel's CG is actually the Z axis, but the wheel is not rotating around it. |
| Neil Wyatt | 07/02/2017 13:31:03 |
19226 forum posts 749 photos 86 articles | Posted by Geoff Theasby on 07/02/2017 12:00:59:
I discovered the Coriolis effect as a child, playing on a roundabout. Trying to kick the central pillar whilst facing inwards, my foot was deflected to the left. Saved from a life of delinquency by the coriolis effect! Reminds me a of an avatar cartoon I saw recently - Mother to errant child: "Look here young, Copernicus, you'll have to learn the world does not revolve around you." Neil |
| Geoff Theasby | 07/02/2017 16:06:04 |
| 615 forum posts 21 photos | You mean I'm not a senile delinquent, even after trying so hard for so long? Oh drat! And double drat!! Geoff |
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- hemingway ball turner
04/07/2025 14:40:26 - *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!










 Register
Register Log-in
Log-in


