A bit of math - lenght of belt in pulley systems.
| Martin Dowing | 29/10/2017 00:52:24 |
356 forum posts 8 photos | @Michael Gilligan Many thanks, your formua seems exact. Had few goes at it and it invariably gives sensible results. They are usually very similar to approximations discussed before but in weird cases approaching extremities there are significant discrepancies. Martin |
| Russ B | 29/10/2017 00:54:25 |
| 635 forum posts 34 photos | sadly I'm 7000 miles from my notes at the minute but I don't do it like this.... I calculate the contact angle overlap on each pulley first (in radians if I recal correct) (if the pulleys are equal the formula should equal zero) - so if one pulley is larger, it's contact will be 1(pi)r+overlap arc, and the small pulley will be 1(pi)r-overlap arc. you can also easily apply inertial forces to the equasion as the belt tries to throw itself off the pulley. you can then start manipulating the figures to see how much pulley overlap is required to transmit the torque you desire (for a flat or vee belt etc) which gives you an idea of where your idler needs to be to create the desired overlap. for a toothed pulley, you'd just drop the friction factor our of the maxiumum torque calcs and assume it's 1:1 with no slip, and just concern yourself with the tension in the taut side to make sure you're not going to snap it. Since you don't have any slippage, adding an idler won't change the results, but common sense tells you need a certain minimum number of teeth engaged and the manufacturer or standard texts will probably dictate a minimum radius anyway. has it been considered that many common toothed pulleys have inherent backlash - and there are a few which specifically dont - hence ideal of automation/cnc
- Sorry I can't give you proper formula - I've googled but didn't find what I need, I've seen other ways but they make it look complex...... see here for the closest but note, because he's using degree's and not radians, i think.... his calcs are significantly more complex/long hand with some slightly more exotic trig functions that im not entirely sure are necessary! |
| Russ B | 29/10/2017 01:02:08 |
| 635 forum posts 34 photos | Well bloody hell..... I think Michael Gilligan has just flashed up half of what I was rambling about while I was typing!!!! Good stuff there in 1.23 and it will easily fit with many other standard calcs surrounding belts
(and just look how much simpler rads make the equation!) Edited By Russ B on 29/10/2017 01:03:05 |
| Michael Gilligan | 29/10/2017 08:03:15 |
23121 forum posts 1360 photos | I think S.K. Bose, and the Publisher deserve credit for a concise and useful book: http://www.alliedpublishers.com/BookDetails.aspx?BookId=94 http://www.alliedpublishers.com/group.aspx MichaelG. |
| SillyOldDuffer | 29/10/2017 09:17:50 |
| 10668 forum posts 2415 photos | Posted by Neil Wyatt on 28/10/2017 22:27:32:
Posted by Martin Dowing on 28/10/2017 20:33:46:
@Neil When I substitute to your equation extreme case where l=1/2 x d1 and d2 = 0 I cannot get sensible resuls. I I think no-one spotted I left a /2 out of the (pi x d2)/2 bit - I've edited the formula. ...Please sir, please sir, I did! Can I have a House Point, please sir! Unfortunately for teacher's pet I was too busy yesterday to point Neil's boob out when it might have helped. Anyway here's two formula from 'Introduction to Mechanical Design, Jefferson and Brooking, New York, 1950'. It's interesting mainly because the second formula calculates the length of a crossed belt and the two formula are similar to those linked by Michael Gillighan. I might have some 'fun' later comparing mine and his. Not tried yet but they may just be different representations of the same maths. Accurately calculating the length of a belt between two pulleys is quite difficult. Obviously the profile of the belt matters. Do you calculate the inner length, the neutral line, or the outer circumference? Etc. Less obvious are the corrections needed when the belt is working; the tension side stretches whilst the other slackens. Therefore the contact arcs on the slack side are increased compared with the stopped condition. Even if the only force on the belt is gravity, the contact tangents on each side of the pulleys are slightly different. And the elasticity of the belt matters - there's no law that says stretch - slack = 0. To add to the brain strain there's a whole bunch of other maths dealing with variations in belt material, power, wear, velocity, pulley diameters relative to speed ratios, crown radii, and belt width. Just for laughs the answers are often modified by 'service corrections' which seem to be rule-of-thumb. For example there are different service factors given for three variants of the Squirrel Cage Motor as applied to each of the 20 types of machinery tabulated. The factors look to be compensating for starting and running jerks on the belt. Electric motors are usually, but not always, kinder to a belt than a steam engine, presumably because the later applies both high starting torque and reciprocating pulses of energy to the belt. I think for practical purposes the approximations are 'good enough'. Dave Edit typos galore
Edited By SillyOldDuffer on 29/10/2017 09:23:42 |
| Neil Wyatt | 29/10/2017 09:44:08 |
19226 forum posts 749 photos 86 articles | Dave, The formula you give for flat belts is the same as mine. It's right for practical situations but these chaps want to encompass overlapping pulleys of zero and infinite radius as well... Neil |
| Martin Dowing | 29/10/2017 10:46:10 |
356 forum posts 8 photos | Neil, Both, estimated and accurate formulas are comparably complex if one has access to trig tables or adequate calculator and wish to work in radians. Extreme cases are used for checking only. I got alarmed because one extreme case where d1=2l and d2=0 would give a result which can be expressed as l = a x pi + b x sqrt(c). However it is obvious that l = pi x d = 2pi x l. It is *impossible* to get an accurate pi x d from the sum of a x pi and b x sqrt(c) if b x sqrt(c) is *not* equal 0. Hence it was immediately obvious for me that you have given an estimate where errors are produced by replacing lenghts of arcs with lenghts of chords or alternatively you have made a mistake. Because I have never done such calculation in the past and I am designing 2 step pulley system meant to work with *the same* belt, I was just wondering what sort of error might be there, just to make sure that fabricated parts (or one of them to be precise) would not go directly to scrap. Indeed, as you say, in normal situation the error is small enough to ignore. Just wanted to make sure. For reference of this forum I will quote an accurate formula from discussed book: l(belt) = pi/2 x (d1+d2) + *alpha* x (d1-d2) + 2 x l x cos*alpha* where: sin*alpha* = (d1-d2)/2 x l and angles are expressed in radians, eg 360deg = 2 x pi. *alpha* is an angle between "squared" situation, eg one where d1=d2 and "triangulized" one, where it is not the case and last point of contact of belt with pulley is shifted by an angle. You do *not* need to know *alpha* a priori. l(belt) means lenght of belt, d1 & d2 means diameters of pulleys and l is a distance between centers of rotation of pulleys. Hope, I have written it clear. Anyway, we have managed to convert something what looks trivial into quite lenghty discussion. It is interesting that an accurate formula is somehow well "hidden" on Internet. Martin Edit: Hey, lets make it now more complicated, get rid of *alpha*, and put it into one final phrase: It is known from secondary school that sin^2*alpha* + cos^2*alpha* = 1 so: cos*alpha* = sqrt{1 - [(d1-d2)/2 x l]^2} so the final, one phrase equation devoid of *alpha* will read: l(belt) = pi/2 x (d1+d2) + arccos*sqrt{1 - [(d1-d2)/2 x l]^2}* x (d1-d2) + 2 x l x sqrt{1 - [(d1-d2)/2 x l]^2} where: *sqrt{1 - [(d1-d2)/2 x l]^2}* reads in radians. Now I will go to do something useful Martin
Edited By Martin Dowing on 29/10/2017 11:25:16 |
| Neil Wyatt | 29/10/2017 14:01:56 |
19226 forum posts 749 photos 86 articles | Don't forget that belts are made to length tolerances so a formula more accurate than the belt is spitting in the wind... |
| SillyOldDuffer | 29/10/2017 14:13:47 |
| 10668 forum posts 2415 photos | Posted by Neil Wyatt on 29/10/2017 09:44:08:
Dave, The formula you give for flat belts is the same as mine. It's right for practical situations but these chaps want to encompass overlapping pulleys of zero and infinite radius as well... Neil Thanks Neil, I suspected it might be but hadn't checked. (And still haven't!) I seem to remember Dr Who destroying a computer bent on world domination by asking it a question about zero and infinity. Dave |
| Michael Gilligan | 29/10/2017 14:22:11 |
23121 forum posts 1360 photos | This may earn me some ridicule on the "when the media poke fun" thread [which is running concurrently, and seems to have developed into sparring about mathematical prowess]; but here goes ... I was pleased to find that *exact* calculation last night; especially as it is comparatively simple. But what delighted me was the realisation that the angle 'alpha' is identical on the two pulleys, regardless of their size. I had never really thought about it before, and it is perhaps not intuitively obvious when looking at a pair of pulleys. This was one of those 'paperclip' moments for me [in that, like the design of the paperclip; it becomes obvious when you've seen it and understood]. MichaelG |
| duncan webster | 29/10/2017 15:11:30 |
| 5307 forum posts 83 photos | Coming at it from trigonometry, centre distance C, big pullet diameter D, little pulley diameter d Angle between belt and centre line a=ASIN((D-d)/(2*C)) straight bit between pulleys L1=C*cos(a) wrap on big pulley W1=pi*D*(180+2*a)/360 wrap on little pulley W2=pi*D*(180-2*a)/360 total length 2*L1*W1+W2 example C=15, D=10, d=5, a=9.5941 deg, L1=14.7902, W1=17.3824, W2=7.8540, total length 54.8168 It's quite a bit harder going the other way, calculating the centres for a given belt length, set up a spreadsheet and use a solve block, or just fiddle wth the centres until you get the right belt length. However as others have said you're better off with some adjustment, so the simpler formulae are near enough. Edited By duncan webster on 29/10/2017 15:12:01 |
| Tim Stevens | 29/10/2017 16:22:05 |
1779 forum posts 1 photos | In the old days of cotton mills and big steam engines you needed to consider an allowance for the droop of each unsupported length, along with the elasticity of the belting. In both these cases a calculation to three places would be nugatory - however much satisfaction it gave to those with maths degrees. Cheers, Tim |
| Gordon W | 29/10/2017 16:27:23 |
| 2011 forum posts | I have two ways to do this :- One - get a bit of rope and wrap round the pulleys, cut rope to length and take it down to belt shop. Two - fit jockey pulley. |
| Muzzer | 29/10/2017 16:34:31 |
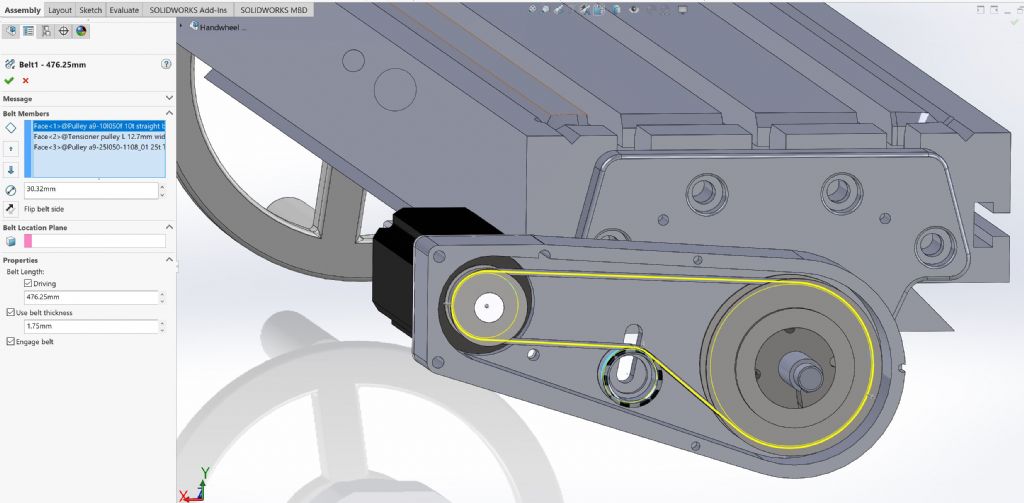
2904 forum posts 448 photos | Duncan - that misses out the thickness of the belt ie where the neutral line is actually located. You need an additional term ("t"?) surely? Here's the cushy way to do it. There are a few other steps naturally but as you can see, it's possible to use a defined belt length to "drive" the position of the tensioner wheel. That way you can place the driving and driven pulley centres to get a sensible range of adjustment. It takes care of the belt thickness but fundamentally it places the neutral axis (yellow) where it needs to be. It also couples the pulleys together if you want to do some completely unnecessary animation. I was impressed by how accurately it worked out for my application. This Youtube tutorial explains i pretty well. Murray Edited By Muzzer on 29/10/2017 16:35:20 |
| duncan webster | 29/10/2017 17:52:57 |
| 5307 forum posts 83 photos | Not if you relate pulley diameters to the pitch (neutral) line |
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - Winter Storage Of Locomotives
04/10/2023 21:02:11 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!











 Register
Register Log-in
Log-in


