Pendulum 'Q' value and measurement methods
| Joseph Noci 1 | 08/08/2023 17:38:29 |
| 1323 forum posts 1431 photos | There are a number of Pendulum threads running and I am doing my utmost to not catch the bug, but it seems I may succumb... It is too tedious to go through paragraph in every post to find out - cannot just search for 'Q' in pendulum or clock posts... What sort of Q values are being achieved by the various Pendulums worked on in these forums? How are you measuring and calculating Q? There are a number or methods it would appear, and some appear contradictory. What is the REAL value of Q in accessing a Pendulum's potential performance? There are many articles, some by real Gurus it would appear, who play down it's usefulness to some or other degree. I understand the Quest for high Q's, but once a sound suspension method is found, drag is reduced to a sensible minimum, etc, what sort of Q value is usable/workable? Obviously aimed at a decent performance pendulum, perhaps not the Short... Edited By Joseph Noci 1 on 08/08/2023 17:40:09 |
| S K | 08/08/2023 17:59:00 |
| 288 forum posts 42 photos | I measured a Q of about 18,500 in my genuinely-free pendulum (no restoring power input). The pendulum was about 24" in length, had about a 1 lb bob, and it was rocking on knife edges: I measured it by counting the number of swings until the amplitude decayed to 1/e (to 36.8%) of its original value. I used a video camera to capture the amplitude of the swings, with an engineer's rule behind the bottom tip of shaft. In a vacuum, Q will go up dramatically, since air resistance becomes a non-issue and essentially the only remaining loss of energy is in the hinge. The value of achieving high Q has been debated, but I have faith that obtaining high Q promotes high performance. |
| Russell Eberhardt | 08/08/2023 18:03:28 |
2785 forum posts 87 photos | Easy way to measure pendulum Q is to set it to swing freely and count the number of periods it takes for the amplitude to fall by 21%. Double it to get the Q. Expect a value of around 10,000 for a good clock pendulum. Russell Edited By Russell Eberhardt on 08/08/2023 18:05:17 |
| Michael Gilligan | 08/08/2023 18:57:36 |
23121 forum posts 1360 photos | I would be interested to know at what starting-angle of swing the pendulum is being checked. It has long been common practice, in accurate clocks, to use very small angles of swing to avoid the effects of circular error … but the practical measurement of the delta reduction must then become increasingly difficult. Mmm MichaelG. |
| Joseph Noci 1 | 08/08/2023 19:28:56 |
| 1323 forum posts 1431 photos | So, we have : number of swings till amplitude = 36.8% of start Number of swings till amplitude fell by 21%, and double the number another source...Number of swings till amplitude is halved, time 4.53. Where do these magic numbers come from? Q actually = total energy / energy lost per swing, but that is difficult to measure...
|
| Russell Eberhardt | 08/08/2023 19:54:44 |
2785 forum posts 87 photos | They are not magic numbers. They come from a bit of mathematics. See for example **LINK** Russell |
| Michael Gilligan | 08/08/2023 20:07:30 |
23121 forum posts 1360 photos | Clever maths … but the resulting value for Q [ upper-right of p5] is woefully low. MichaelG. |
| SillyOldDuffer | 08/08/2023 20:25:21 |
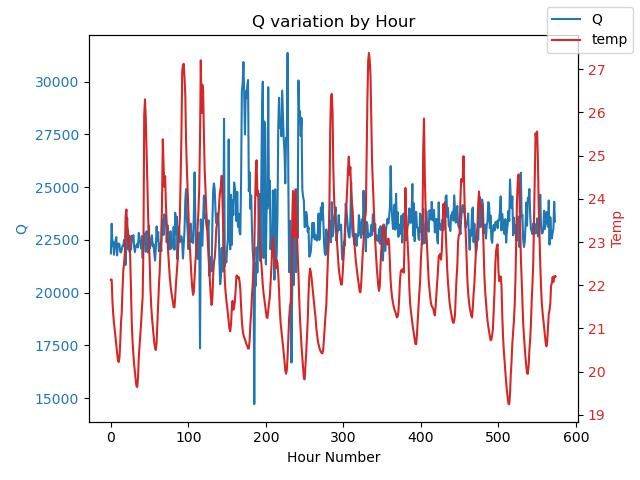
| 10668 forum posts 2415 photos | My experimental pendulum reports 21399 It's calculated using the bandwidth definition because logging a pendulum with a microprocessor produces all the data needed to calculate bandwidth. Much easier that measuring decay and, I think, measuring impulsed Q is more useful than measuring free-swinging Q. Clock pendulums are impulsed, not free. Bandwidth is calculated from the 29.3, 50,0 and 70.7 percentiles. Easy in Python because numpy has a percentile function. Where tickArray is a list of periods: h, l, r = np.percentile(tickArray, [70.7, 29.3, 50] ) I see Q as a measure of the purity and stability of an oscillator, where high Q means it produces close to one frequency only. Real oscillators do not produce a single frequency, they wobble around it, and they are likely to drift. I've noticed good long-term time-keeping can be got from a low Q pendulum - less than 5000. I believe it's because wobble errors tend to average out, and aren't obvious unless the clock has a high resolution display. As most pendulum clocks only display to the nearest second or minute, low Q may not matter because the error is invisible and doesn't accumulate. However, high Q becomes important whenever a clock must be high-precision or high-resolution. I need a high Q pendulum because I'm chasing milliseconds and below, but what I'm doing is bonkers! One of the other threads asked if Q varies. Normally Q is measured once by simple methods and assumed to a constant. My pendulum's Q isn't! The data suggests the Q of my pendulum varies between about 15000 and 31000. The red line shows temperature and I think I see a relationship - after a lag, temperature causes Q to vary. Far from convincing though - I don't know what causes this. Hard to think why Q should repeatedly peak over a 100 hour period. Perhaps the moon did it! Like as not other pendula do the same, because mechanical or environmental changes are likely to affect the purity of the signal. Anyone happy with their clock is advised not to look too closely! That way lies madness. Nature conspires in many ways to subtly alter the period of a pendulum despite the clockmaker's best efforts. Dave
|
| duncan webster | 08/08/2023 20:44:58 |
| 5307 forum posts 83 photos | Posted by Joseph Noci 1 on 08/08/2023 19:28:56:
So, we have : number of swings till amplitude = 36.8% of start Number of swings till amplitude fell by 21%, and double the number another source...Number of swings till amplitude is halved, time 4.53. Where do these magic numbers come from? Q actually = total energy / energy lost per swing, but that is difficult to measure...
Probably something to do with exponential decay |
| S K | 08/08/2023 21:11:42 |
| 288 forum posts 42 photos | Posted by duncan webster on 08/08/2023 20:44:58:
Posted by Joseph Noci 1 on 08/08/2023 19:28:56:
So, we have : number of swings till amplitude = 36.8% of start
Count the swings to 36.8% ... and then multiply that by 2*Pi. (Sorry, I left that out somehow.)
|
| Joseph Noci 1 | 08/08/2023 22:04:26 |
| 1323 forum posts 1431 photos | Posted by Russell Eberhardt on 08/08/2023 19:54:44:
They are not magic numbers. They come from a bit of mathematics. See for example **LINK** Russell 'Magic' was just a bit of a dig at the variation of methods. Qilin Xue's maths appears sound but I would presume the other methods have some mathematical basis as well? Yet they would appear to give very different results? The 'other' source I quoted comes from this link : LINK |
| John Haine | 08/08/2023 22:26:44 |
| 5563 forum posts 322 photos | The Shortt free pendulum in vacuum IIRC had an estimated Q of ~100,000. My tungsten bob pendulum has a measured Q around 24,000 or maybe more at lower amplitude. This measured by run-down tests over a period of hours. Bateman's clock is about 12,000. Classic paper by Bateman has a graph plotting accuracy against Q for a wide range of clocks from watches to atomic and showing inverse correlation over several orders of magnitude. But Clock B only in the 4000 - 5000 range for complicated reasons. So Q is not the whole story. There are many ways to measure and calculate Q but they are all consistent.
Edited By John Haine on 08/08/2023 22:27:39 |
| S K | 08/08/2023 22:33:50 |
| 288 forum posts 42 photos | All of the different swing-counting methods, e.g. "count swings until X% then multiply by constant Y" should yield the same results (I haven't checked, though). It wasn't said, but I presume SOD's measurement was in a partial vacuum? I doubt that a pendulum's Q should change by 50% just due to temperature. I'd think Q certainly could change that much if the air pressure was changed, though. Barring that, I'd rather suspect that instantaneous measurements of Q done that way will be noisy. By comparison, the counting methods have averaging of many hundreds of swings built-in.
|
| Joseph Noci 1 | 08/08/2023 23:33:26 |
| 1323 forum posts 1431 photos | Thanks Chaps - more reading to do!
|
| Michael Gilligan | 09/08/2023 20:02:04 |
23121 forum posts 1360 photos | Nothing new here: **LINK** https://www.statisticshowto.com/calculus-definitions/damped-sine-wave/ Just standard statistical stuff, nicely presented. MichaelG. |
| SillyOldDuffer | 09/08/2023 21:24:28 |
| 10668 forum posts 2415 photos | Posted by S K on 08/08/2023 22:33:50:
... It wasn't said, but I presume SOD's measurement was in a partial vacuum? I doubt that a pendulum's Q should change by 50% just due to temperature. I'd think Q certainly could change that much if the air pressure was changed, though. Barring that, I'd rather suspect that instantaneous measurements of Q done that way will be noisy. By comparison, the counting methods have averaging of many hundreds of swings built-in.
Ah, no.
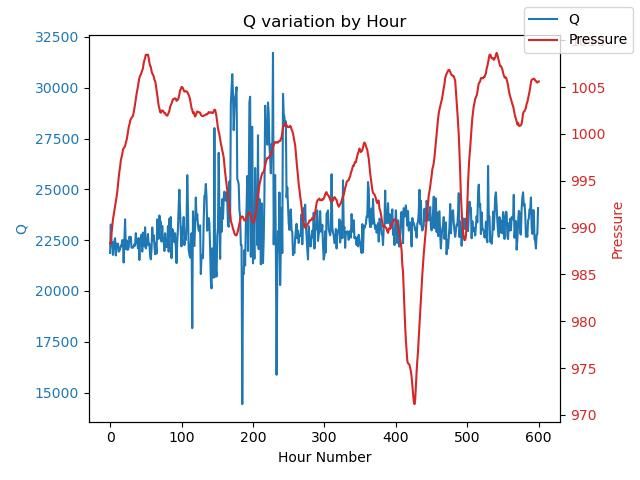
Is the variation pressure related? I don't think so, here's the graph: Date-times that match the Hour Numbers above: clockStart = 2023-07-15 20:30:03 (Hour zero) (ClockEnd is finish time as measured by my clock, ActualEnd is the same finish according to Network Time Protocol. On my set-up NTP is no worse than about 100mS different from Atomic Time, and is normally better, roughly 25mS The Counting and Bandwidth methods produce slightly different results. Doesn't matter, I think, because Q-factor is more indicative than absolute. Q gives a good idea of pendulum quality, but is far from the whole story. Allan Variation is what's needed for that, but despite several attempts I still don't understand it! If anyone can explain the Wikipedia Article to me I shall be eternally grateful. Dave
|
| Michael Gilligan | 09/08/2023 21:45:50 |
23121 forum posts 1360 photos | This is not a criticism, Dave … far from it ! But something is nagging me: By [ quite understandably] scaling your pressure graph from 970, are you perhaps exaggerating its significance ? … what would it look like if you scaled it from zero ? MichaelG.
|
| S K | 09/08/2023 22:34:22 |
| 288 forum posts 42 photos | SOD, I know you believe you are measuring Q, and you are getting "numbers," but I don't believe you are actually measuring Q. The old "garbage in, garbage out" problem, to my eye. If your data was Gaussian and well behaved, and if the obtained value of Q was stable, maybe, but at this point none of that seems evident. Also, I am not sure you are using thousands of samples. Sure, you are collecting thousands, but per Q measurement you are throwing nearly all of them out after selecting only a few (I don't know the details, however, so I could be wrong on this point). In addition, you are subtracting two numbers that are very close together from each other, getting a very small number (i.e., 6 or so orders of magnitude smaller), and then dividing that very small number into a comparatively large one again, tempting the gods of mathematical fate. In this scenario, minute deviations can cause huge impacts on the end result, as it seems you are seeing. Try using the decay method to check. It can't be that hard, others have done it, and the decay method is much more intuitively related to the loss of energy per swing anyway. And also, the value of Q obtained this way should be quite stable from trial to trial (as I believe one would expect from a macroscopic pendulum of this sort).
Edited By S K on 09/08/2023 23:02:19 |
| duncan webster | 10/08/2023 01:19:49 |
| 5307 forum posts 83 photos | I'd expect Q to change with atmospheric pressure and perhaps humidity. Intuitively I'd go for run down to measure it, but intuition based on little actual experience can be dangerous. |
| S K | 10/08/2023 01:53:58 |
| 288 forum posts 42 photos | Duncan, yes, higher pressure and (probably) humidity should reduce Q. But if I'm reading the graph right, a 3.5% atmospheric pressure change is plotted against a 100% change in Q. |
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - Winter Storage Of Locomotives
04/10/2023 21:02:11 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!










 Register
Register Log-in
Log-in


