A not-so-new Pendulum formula
| Michael Gilligan | 09/01/2021 00:13:33 |
23121 forum posts 1360 photos | As we have several members interested in Pendulum Clocks, I thought I would share this [which I only stumbled-across today] : **LINK** http://leapsecond.com/hsn2006/pendulum-period-agm.pdf MichaelG. |
| Gary Wooding | 09/01/2021 07:56:02 |
| 1074 forum posts 290 photos | Fascinating. |
| David Millar 3 | 09/01/2021 09:06:00 |
| 28 forum posts | That's brilliant. I hadn't heard of a geometric average before. Everyday's a school day! |
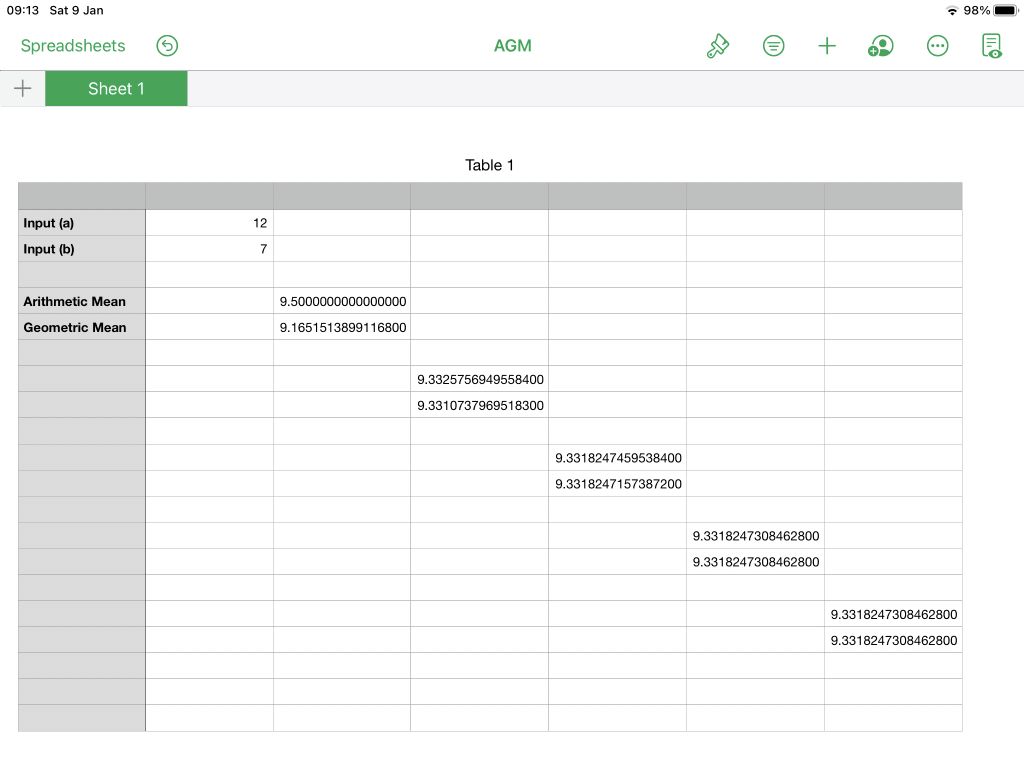
| Michael Gilligan | 09/01/2021 09:20:54 |
23121 forum posts 1360 photos | I did a quick check ... and he’s right about the Means converging in just a few iterations So this looks like it might be very useful indeed MichaelG. . < click for larger image > |
| Martin Connelly | 09/01/2021 09:23:46 |
2549 forum posts 235 photos | I'm being picky but: Even though the formula is exact as soon as you start calculating the mean of a rational and an irrational number it loses this exactness. It is only exact as long as you compute the square roots to an infinite number each time (unless the number is a perfect square to start with). As long as the irrational numbers are truncated it is still an approximation. It may be a good and useable one but perhaps this approximation in the calculation should have been pointed out in the written paper. Martin C |
| John Haine | 09/01/2021 10:28:51 |
| 5563 forum posts 322 photos | It's worth noting that for practical clock pendulum amplitudes, say up to 10 degrees, the difference between the AGM formula and the usual "A^2/16" approximation to the circular deviation is very very small: 3.3 usec for a 1 second period and 10 degrees. I've done pendulum simulations for the order of amplitude used in "Clock B" and compared them to simple formulas based on the same approximation with virtually identical results. Where the AGM really is useful is for methods where you need to quickly compute elliptic integrals. One example is designing very selective LC filters, where there are formulas for the component values that incorporate elliptic integrals. Once you needed to have extensive tables of these, but now they can be calculated more accurately in a few lines of code. |
| Michael Gilligan | 09/01/2021 10:37:50 |
23121 forum posts 1360 photos | Very true, Martin .... but this does get us [with very little effort] several orders of magnitude beyond the classic ‘simplified formula’ which only works for small swings. What excites me about it is that it’s accurate [or trivially inaccurate] for large angles. MichaelG. . P.S. __ The title of the original 2008 paper [see Further reading] is: Approximations for the period of the simple pendulum based on the arithmetic-geometric mean Edit: ___ The link appears to be dead, but this one works for me: Edited By Michael Gilligan on 09/01/2021 10:55:24 |
| Michael Gilligan | 09/01/2021 10:44:24 |
23121 forum posts 1360 photos | Posted by John Haine on 09/01/2021 10:28:51:
. . I am particularly interested in larger swings than that, John Huygens, Harrison, et al ... [pendulum has ‘dominion’ and all that] MichaelG |
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - Winter Storage Of Locomotives
04/10/2023 21:02:11 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!










 Register
Register Log-in
Log-in


