Is Plastow 44T 6D.P bevel gear - 3" Fowler

Hello!

I am just at the point of machining the bevel gears for the 3" Fowler.

I am using Ivan Laws Gears and Gear Cutting for all terminology and calculations.

I will be cutting the gears using Ivan Laws parallel depth method on page 106-111

Now H.R Plastow calls for a 44T Crown wheel and 9T Pinion both 6D.P.

This gives a P.C.D of 7.333"

The problem arises when you look at the distance between the backs of the Pinions. This is stated as 7.969"

Now the P.C.D can't be referring to a True Bevel Gear (True P.C.D of wheel as stated by Ivan Law page 46) as this would make the O/D of the Crown wheel far too small. It also can't be referring to Parallel depth Bevel gears (P.C.D of small end page 106) as this would mean the tooth face is only 5/16" long!

If I use N/D.P I find that 37T gives a small end P.C.D of 6.166"

This allows a tooth face of 0.86" and an O/D of 7.953, which is pretty much perfect for the Distance between the backs of the pinions.

My question is am I missing something here? Is 44T correct and I am being stupid or did Plastow get something wrong and my 37T is correct? I have seen the other thread referring to Bevel gears and ensured I Have changed the Sin to Cos where required but I still get the same result.

Help would be appreciated before I make a lot of cast iron mess!

John

Edited By JasonB on 22/10/2020 11:44:35

This is a general query about bevel gears.

I ave been looking at these for use in traction engines, but wonder why they have to be bevel gears, won't the contrate (as in Meccano gears) type work fine? Ok, not correct to scale, but much easier to cut, and not as if 5rpm is going to worry them. Hidden away inside the differential so not visible anyway.

How many pinions in the design? Assuming that the pinions are evenly spaced then the number of teeth on the gear needs to be divisible by the number of pinions. So 37 teeth must be wrong as 37 is a prime number. If 44 is correct that implies 2 pinions as 44 is not divisible by 3.

Were the gears orginally designed using the parallel depth method? If not then your calculations are meaningless. Normal straight tooth bevel gears, with tapered teeth, are designed using the DP at the outer face. However, parallel depth bevel gears are designed using the DP at the inner face, so a standard involute cutter can be used.

It's difficult, if not impossible, to re-design normal bevel gears to be parallel depth while keeping the outer PCDs the same and also making the DP at the inner face an integer.

When I was looking at the bevel gears for my traction engine governors I started to re-design using the parallel depth method. But keeping to standard integer values of DP at the inner face simply didn't work. If I was going to design and CNC machine the gears anyway then there was no point in using the parallel depth method. So I stayed with normal straight tooth bevel gears:

Andrew

Certainly, although I don't know if it was ever used full size. Some late Aveling and Porter road rollers used an arrangement of spur gears and pinions to achieve a differential function without the need for bevel gears.

Andrew

Fowlers tended to use two pinions though mine runs 33T on the wheels and 11T on the pinions

EDIT I see from the Plastow boot that diff gears are CP and plain drivetrain gears DP he also talks about them best being done on a gear shaper so drawings probably don't suit parallel depth method.

J

PS Good to see you back Andrew.

Edited By JasonB on 22/10/2020 12:00:53

Andrew,

The design calls for 2 pinions exactly diametrically opposite.

Why does the Crown wheel have to be divisible by the amount of Pinions?

So I am only able to cut the bevel gears using the parallel method in Ivan Laws book. And using his procedure, 44T Crown wheel doesn't seem to fit the design?

Cheers,

John

Was paper really expensive when these drawings were done? Cluttered drawings lead to mistakes and these are very cluttered.

Martin C

Bit here about cutting the gears and says 44T & 9T

Thanks Jason, unfortunately the article does not explain how the Crown wheel can have 44T and still be the correct size.

Regards,

John

If we place one pinion at the top of the bevel gear then the teeth on the pinion will be in a set, but arbitrary, position. If we now place the second pinion 180° apart then the orientation of the teeth on the second pinion will depend upon the number of teeth on the bevel gear. If the number of teeth on the bevel gear is divisible by two then the orientation of the pinion will be the same top and bottom and the second bevel gear will fit as the teeth on the pinions will be oriented the same top and bottom. However if the number of teeth is not divisible by two then the orientation of the bottom pinion will be different. So the alignment of the pinion teeth will be different between top and bottom pinions and the mating bevel gear will not fit.

Andrew

Edited By Andrew Johnston on 22/10/2020 14:36:21

It won't. As I mentioned straight tooth bevel gears are designed using the DP at the outer face while parallel depth bevel gears are designed using the DP at the inner edge. So if you design a 6DP parallel tooth bevel gear with 44 teeth the pitch circle diameter (PCD) will be correct at the inner edge. But at the outer edge the DP will be smaller than 6 (depending upon the face width) and the PCD will be correspondingly larger.

Take the following with a pinch of salt. While I've designed and made a fair number of bevel gears I've never needed to use the parallel depth method. You need to set the outer DP to 6 and then work out what the DP will be at the inner edge. Presumably in proportion to the face width and cone distance. Once you have a value for the inner DP (almost certainly not an integer value) you can then design the gears as per the book. Since the inner face DP will not be standard you will need to make your own cutter. I don't know if the parallel bevel gears so designed will have the same back face to back face dimensions as the original gears. The values should be close, but I don't know if they will be identical.

On MEM Don Darbonne (Don1966 I think) has published an Excel spreadsheet for automating gear calculations including parallel depth bevel gears.

Andrew

Andrew,

"You need to set the outer DP to 6 and then work out what the DP will be at the inner edge."

Any idea how I go about this haha?

Regards,

John

Though in the case of my Fowler with two pinions and 33teeth on the wheels it does fit. On one wheel the tooth of one pinion and the valley of the other will be engaged and the opposite for the other wheel.

I wondered if that might be the case when I was composing my reply. May be it also depends upon the number of teeth on the pinion? I recall a post on here, or TT, where the poster had made a bevel gear with a tooth count that was not divisible by three so that his differential would not fit together. He got around the problem by spacing the three pinions at unequal angles around the circumference.

Andrew

So it seems a 44T 6.D.P parallel depth tooth, Crown wheel, to the dimensions specified does not exist?

And as Jason says, on an odd number Crown wheel, the pinions will be in opposite positions which will match up with the opposite Crown wheel?

So I can use my plan of a 37T Crown wheel?

John

Starting with 44 teeth and 6DP for the design as published we get a PCD at the outer edge of the bevel gear of 7.333". The face width is given as 57/64". If we subtract twice that from the outer PCD we will get the inner PCD, ie, 5.552". If we divide 44 by the inner PCD we get the DP at the inner face. I make it 7.925. That's close enough to 8 to wonder if it might be worth tweaking the face width to make it exactly 8. The PCD for a 44 tooth 8 DP bevel gear is 5.5". Subtracting that from the PCD at the outer edge and dividing by two will give the new face width. I make the answer 0.9167" or just under 59/64".

So if you increase the face width to 0.9167" then you should be able to cut the gears with an 8DP cutter, using the correct number of cutter according to Tregold's approximation. How to calculate the cutter number is in the book, but not described as Tregold's approximation, nor why it is an approximation.

Caveat: I'm making this up as I go, and I've just started my second beer. I expect Jason will be along to correct me if I've got it wrong.

Andrew

Hi

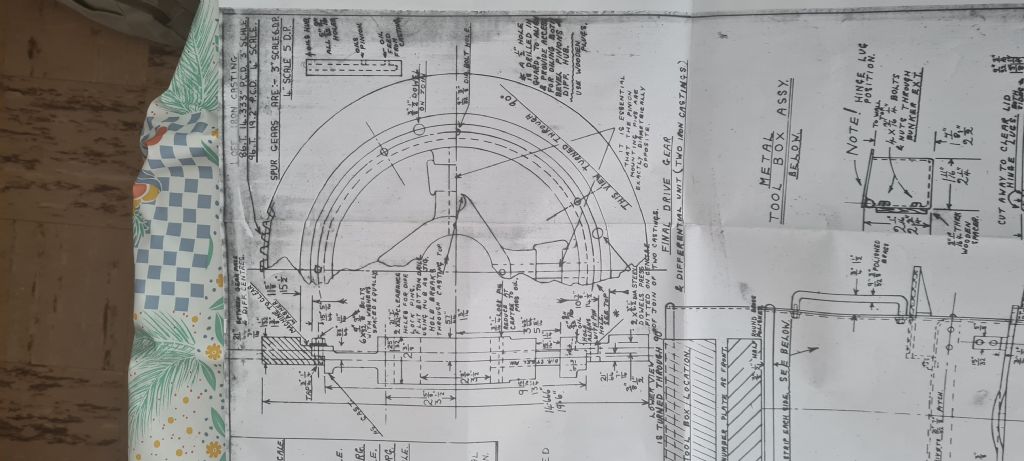
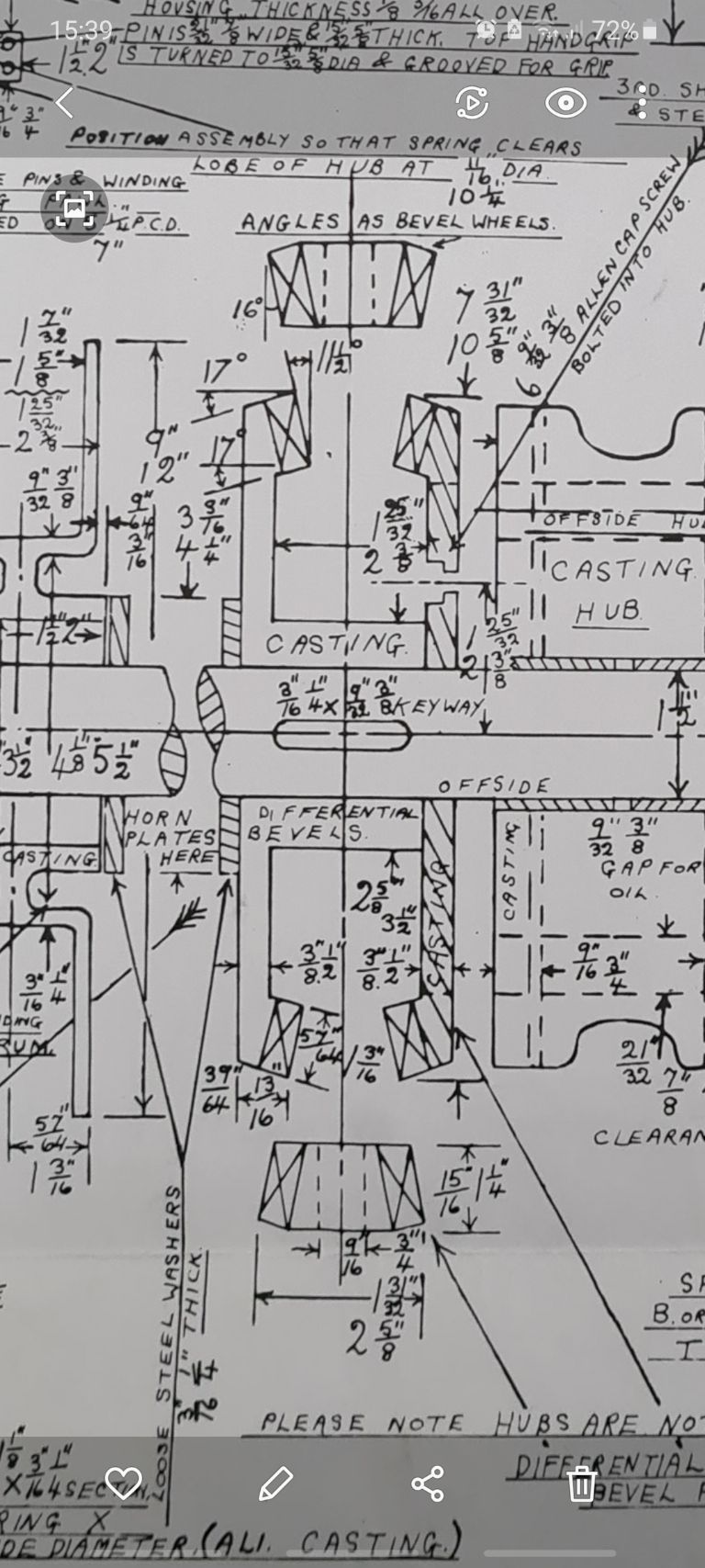
The problem that you have with these gears you may not
be able to solve using the parallel depth method.
As Andrew indicated earlier generated bevel gears
are calculated from the outside of the cone and
parallel depth from the inner cone.

The diagrammatic representation of the 44 tooth gear here at
6 DP shows how the gear reduces in diameter as the DP
number rises ,to obtain the gear face width of 57/64 inch
(.890 inch) would mean the starting point for the calculation
would be 7.871 DP . This would be possible to do
using the calculation to make cutters as seen in the book
gears and gear cutting providing that you can find tables
that go down to 9 tooth .The tables on page 115 show
these at 30 deg pressure angles down to 10 tooth which may do.
The minimum tooth count that you can cut parallel depth
bevels at 20 deg pa is 12 tooth using the tables in the book and that is providing that is a
pair or 12 and 13 tooth pair ,as the angle changes the minimum
size creeps back up to 17 tooth otherwise under cutting is
present at the inner root as seen here in this photo
of about 16 and 31 tooth set.

John

Hi

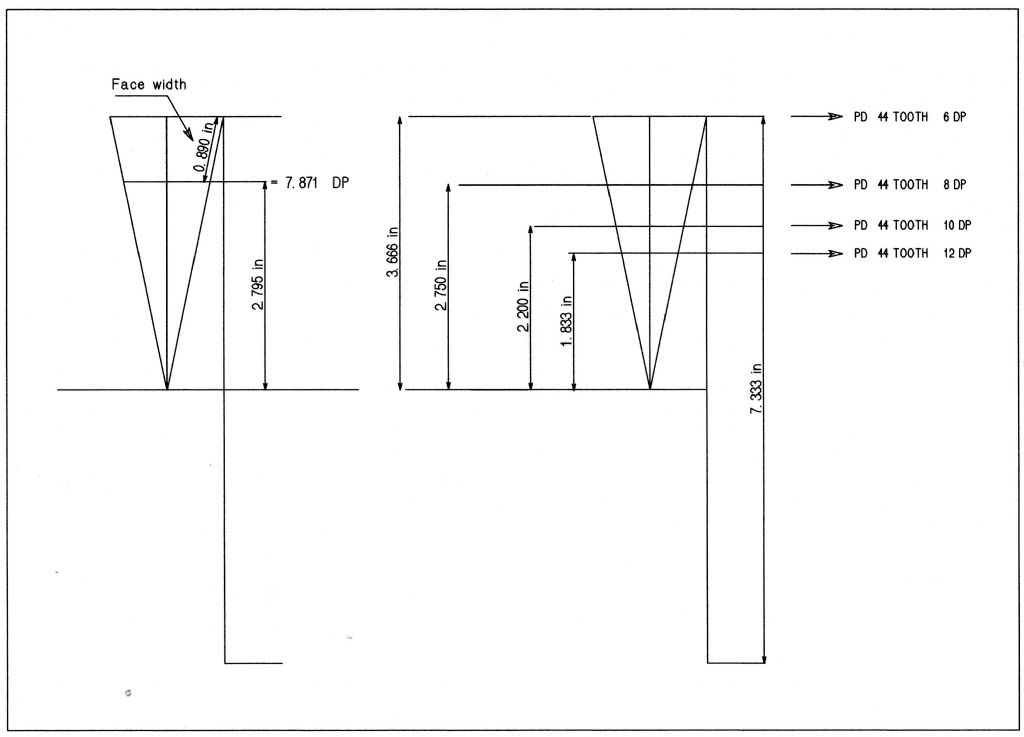
Further on from yesterday's post the size of 7.871 DP
this is very close to 3.25 module at 7.815 DP ,Aliexpress do
sell Mod 3.25 cutters at just under £10 each .
The No 1 cutter goes down to 12 teeth at the angle of the 9 tooth
bevel gear the equivalent spur gear tooth count would be about 9.28
changing to 10 tooth gear you get to about 10.3 teeth and a 11 tooth
gear would be 11.4 tooth so not far off from the 12 tooth minimum
count of a No 1 cutter you might get away with this.
If you can live with the slightly larger gear it might be worth a try
at just under £20 for the cutters

John