Isochronous knife edge suspension?
| SillyOldDuffer | 07/09/2023 10:27:16 | |
| 10668 forum posts 2415 photos | Posted by david bennett 8 on 07/09/2023 04:03:17:
... I think that this is another example of a close look at what is actually happening serves better than blindly following the accepted formulae. dave8 Formula are models attempting to simulate the real world. They are correct, or at least "good enough" provided their limitations are recognised. The period formula assumes that the pendulum is rigidly mounted on solid ground, has a frictionless suspension, temperature and pressure are constant; and there are no other external forces in play. My cat is a menace! Suspending a pendulum from a magnetically attracted roller is likely to cause trouble because, even if it causes the bob to swing isochronously, the suspension is unlikely to be rigid or low friction. (Reluctance is Friction) The energy lost due to friction whilst bending the suspension scuppered Huygens cheeks, even though the geometry produces isochronous beats:
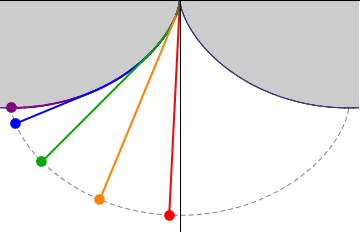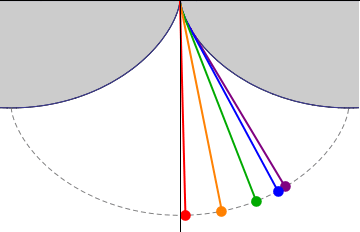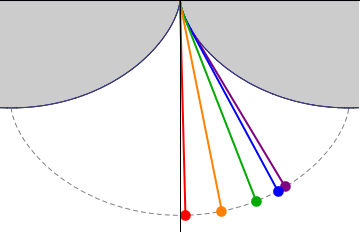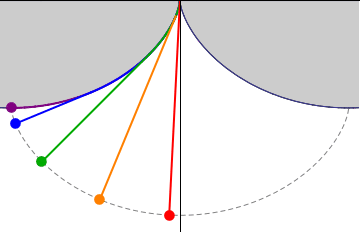
Easier to build a clock with an ordinary pendulum and run it at low amplitude (red example above). Near bottom dead centre the curve followed by the bob is nearly isochronous. It's a good practical compromise because the amplitude error is small. I believe Fedchenko is the only person to make a satisfactory low friction isochronous suspension. So far! All practical clocks break the pendulum formula to some degree because real-world engineering is always imperfect. Mathematical models are still useful though. Comparing the behaviour of an engineered solution with that predicted by formulae perfect in theory often reveals where engineering effort on improvements is most needed. Or the experiment might reveal that the formula isn't quite right, and it has to be changed. Practical men are far too inclined to dismiss theory, leaping to the conclusion that a few failed misunderstanding prove conclusively that 'expurts' know nothing. Practical men get stuff wrong too. The shortcomings of formula as models are the subject of much humour in the scientific community, notably the many variations of the Spherical Cow joke. This example pinched from Wikipedia. Milk production at a dairy farm was low, so the farmer wrote to the local university, asking for help from academia. ... Shortly thereafter a theoretical physicist returned to the farm, saying to the farmer, "I have the solution, but it works only in the case of spherical cows in a vacuum."
I think the magnetic suspension idea has merit, but it will be hard to make it work. Dave
| |
| John Haine | 07/09/2023 11:42:54 | |
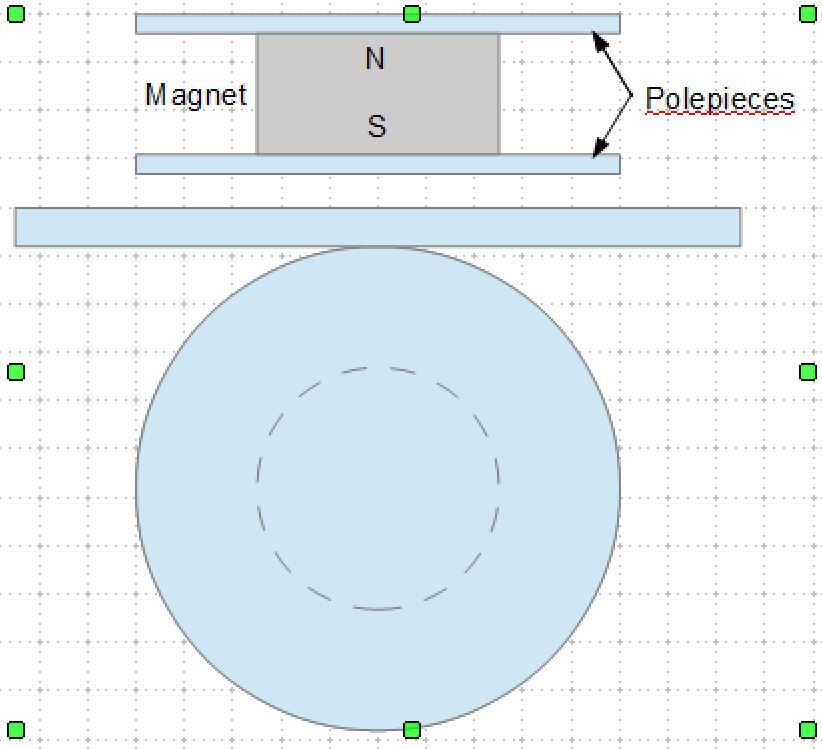
| 5563 forum posts 322 photos | "All models are wrong, but some are useful." https://en.wikipedia.org/wiki/All_models_are_wrong Magnetic "reluctance" has a specific meaning, being the relationship between field (measured in amps/metre) and flux (tesla) in a magnetic circuit. It isn't a measure of the magnetic attraction or "reluctance to let go". This is my mental picture of the arrangement. The rollers are two soft steel discs that form polepieces for a strong short cylindrical magnet mounted coaxially between them. If the contact is good virtually all the flux from the permanent magnet will flow through the polepieces, and establish a magnetic field in the space outside them, mainly concentrated in the air gap. The lower picture shows this hanging from a flat soft magnetic plate. Since the plate and discs are in contact at the tangent point, most of the actual flux will flow through this point as that is the path of minimum reluctance. There will be some flux in the gap close to the contact point but it will fall off rapidly with distance. If there was any imbalance between the forces on each side of the contact point then the roller would move on its own - symmetry ensures it won't move. In a real suspension the radius of the discs would be much larger and we will only need a small proportion of the circumference, but if we made sure that there was enough that the movement of the contact point is only a small proportion of the width I would guess there would still be no net magnetic force - given a suitable field analysis program we could compute this. So I don't think that it's obvious that the system won't work at least from a magnetics point of view. Edited By John Haine on 07/09/2023 11:43:50 | |
| duncan webster | 07/09/2023 13:31:30 | |
| 5307 forum posts 83 photos | I'm with John, I think it works in principle. The difficulty is stopping it going walkies. My only suggestion is a set of very thin metal tapes wrapped round curved members coaxial with the pole pieces. | |
| Tony Jeffree | 07/09/2023 13:41:13 | |
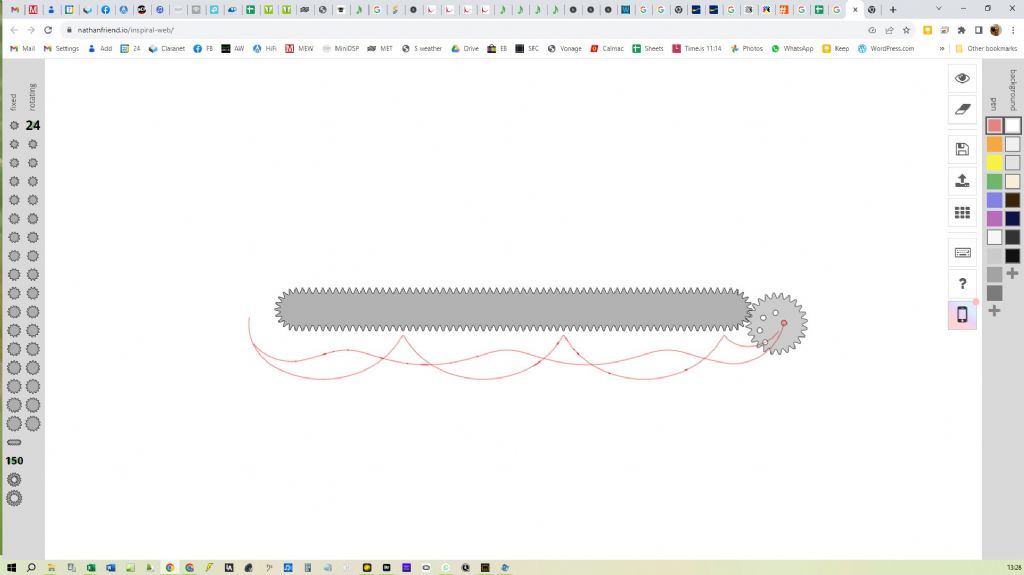
569 forum posts 20 photos | Just in case there is still any doubt about what is going on here, it might be worth digging out your old Spirograph set and playing with that. I found an online Spirograph sim that illustrates the point with a tad of imagination: The two traces in the pic are formed by (1) using a point close to the circumference of the roller (trace near enough cycloidal), and (2) a point close to the centre of the roller (trace approaching a flat line). It will be no surprise that if you trace the path of the centre of the roller, it would actually be a straight line. What the sim doesn't allow, but which you could do with a real spirograph, is to strap a larger wheel onto the smaler one to allow you to see what happens when you trace a point that is outside the circumference of the roller - e.g., a point on the "bob". It doesn't take much to visualise what the trace looks like - apart from anything else, on each full rotation it passes through the horizontal plane, performs a retrograde loop, and then passes back through the horizontal plane. | |
| John Haine | 07/09/2023 13:43:25 | |
| 5563 forum posts 322 photos | Tony, nice! What is the tool called please? | |
| Tony Jeffree | 07/09/2023 13:49:00 | |
569 forum posts 20 photos | https://nathanfriend.io/inspiral-web/ Incidentally, my observation that the centre of the roller follows a straight line should tell you that the centre of mass of the bob needs to be on the circumference of the roller (earlier on there was some uncertainty as to whether the roller radius or diameter should equal the pendulum length - clearly it has to be the diameter, or the bob would travel a straight line path.) Edited By Tony Jeffree on 07/09/2023 13:52:47 | |
| Tony Jeffree | 07/09/2023 14:04:58 | |
569 forum posts 20 photos | Of course, a moment's thought about the wheels on a car would have brought you to the same conclusion. A point on the tread follows a near-enough cycloidal path (give or take the flexibility of the tyre), but you'd better hope that the wheel axle doesn't follow a cycloid, or it is going to be a rather bumpy ride! Edited By Tony Jeffree on 07/09/2023 14:05:35 | |
| Michael Gilligan | 07/09/2023 15:54:32 | |
23121 forum posts 1360 photos | Tony As you have so obviously got a grip on all of this … Would you please do me the favour of reading Huygens’ description of his layout process; and then explain exactly the result what he is doing ? Something in it doesn’t quite ring true The English translation of text is on the page that I posted
But, for everyone’s convenience, I will post the transcription of the Latin and IanBruce’s translation shortly. It all seems consistent in itself, but … MichaelG. | |
| Michael Gilligan | 07/09/2023 15:57:20 | |
23121 forum posts 1360 photos | Huygens:
Super tabula plana affigatur regula A B, semidigiti crassitudine. Deinde fiat cylindrus C D E eadem illa altitudine, diametrum vero baseos, dimidiae perpendiculi longitudini, aequalem habens; sitque F G H E fasciola, seu potius bractea tenuis, affixa regulae in huic F, cylindro vero in circumferentiae puncto aliquo E, ita ut partim huic circumvoluta sit, partim extendatur juxta latus regulae A B. Cylindro autem infixa sit ferrea cuspis D I, pauxillum ultra basis inferiorem prominens, atque ita ut circumferentiae ejus exacte respondeat. [p. 11] His ita se habentibus, si cylindrus secundum regulum A B volvatur, bracteolae tantum FG crassitudine intercedente, eaque semper quantum potest extensa, describet cuspis I subjecto tabulae plano lineam curvam KI, quae Cyclois vocatur. Circulus vero genitor erit CDE, cylindri adhibiti basis. Quod si jam laminam KL ad regulam A B applicuerimus; exarata primum ea cycloidis portione K I, invertemus deinde ipsam, & in superficie adversa similem lineam K M, ab eodem puncto K egredientem, incidemus. Tum figuram MKI, accurate secundum, lineas istas, efformabimus, cui figurae lamellarum interstitium aptari oportet, inter quas per pendiculum suspenditur. Sufficiunt autem ad horologiorum usum portiones exiguae arcuum K M, K I; reliquo flexu inutili futuro, ad quem perpendiculi filum accedere non potest. Verum, ut mirabilis lineae natura atque effectus plenius intelligantur, integras semicycloides KM, KI, alio schemate hic exprimere visum fuit, inter quas suspensum agitatumque Pendulum KNP, diametri circuli genitoris duplum, cujuscunque amplitudinis oscillationes, usque ad maximam omnium per arcum MPI, iisdem temporibus confecturum sit: atque ita, ut appensae spherae P centrum, in linea M P I, quae & ipsa cyclois integra est, semper versetur. Quae proprietas insignis nescio an alii praeter hanc lineae data sit, ut nempe se ipsam sui evolutione describat. Haec autem quae dicta sunt, in sequentibus, ubi de descensu gravium, deque evolutione curvarum agemus, singula demonstrabuntur. [p. 12]
| |
| Michael Gilligan | 07/09/2023 15:58:39 | |
23121 forum posts 1360 photos | Ian Bruce:
Upon a flat table the rule AB is fixed, half a finger wide. Then there is present a cylinder C D E truly with the diameter of the base equal to half the length of the pendulum; and F G H E is a small bandage, or better a thin metal foil, fixed to the rule at the point F of this, and to some point of the circumference of the cylinder E, thus in order that it shall be partially wrapped around the cylinder alongside the rule A B. Moreover a sharp iron point DI shall be fixed to the cylinder, projecting a little below the base, and thus in order that the circumference of the cylinder corresponds exactly to it. [p. 11] Thus with these in place, if the cylinder is rotated along the rule A B, with the metal foil in between as far as FG, and with that always extended as far as possible, the sharp point I applied below on the plane table will describe the curved line KI, which is called the cycloid. Truly the circle CDE is the originator of the curve, applied to the base of the cylinder. Since if now we apply the plate KL to the rule A B ; that first part of the cycloid KI is traced out, then we invert the plate, and in the facing surface the similar curve KM is inscribed, arising from the same point K. Then we will have formed the figure MKI, following these lines carefully for the figure of the plates it is necessary to adapt, through the gap between which the pendulum is hanging. Moreover the small portions of the arc KM, KI are sufficient for the use of the clocks ; with the remainder of the curve not to be used in the future, and to which the string of the pendulum does not have access. Truly, in order that the wonderful nature of the line and the effect may be understood better, the whole semicycloids KM and KI, here seen to be expressed by another diagram, between which the pendulum KNP is suspended and moving, [of length] twice the diameter of the generating circle, and the oscillations of any amplitude, as far as the largest of all through the arc MPI will be made in the same times : and thus, so that the centre P of a sphere hung on, is always moving to and fro on the line M P I which is part of a whole cycloid. I do not know of any other line with this conspicuous quality, except for this given line, as truly it describes its own evolute. Moreover these things which have touched on, concerning the descent of the weight and the evolute of the curve, we will go through and each will be explained in what follows. [p. 12] | |
| Michael Gilligan | 07/09/2023 16:02:55 | |
23121 forum posts 1360 photos | The translation is obviously into spoken English, but the important words appear to correspond nicely to the Latin. So the big problem is: with the diameter of the base equal to half the length of the pendulum MichaelG. | |
| david bennett 8 | 07/09/2023 16:28:00 | |
| 245 forum posts 19 photos | Visualise a series of concentric circles, each distorted at the base by their appropriate cycloid . draw that on a card and pin it's centre to the axis of the 2p . Compare pendulum paths of a large circle and a small one (2p size ) dave8 Edited By david bennett 8 on 07/09/2023 16:28:54 | |
| david bennett 8 | 07/09/2023 17:50:36 | |
| 245 forum posts 19 photos | John, I was aware of problems with using "reluctance",but I was using in the non-scientific way. I did search for another word to convey my meaning, but still cannot think of one. dave8 Edited By david bennett 8 on 07/09/2023 17:51:06 | |
| SillyOldDuffer | 07/09/2023 18:25:12 | |
| 10668 forum posts 2415 photos | Posted by david bennett 8 on 07/09/2023 17:50:36:
John, I was aware of problems with using "reluctance",but I was using in the non-scientific way. I did search for another word to convey my meaning, but still cannot think of one. dave8 ... Neither can I, which is why I said your reluctance is friction, in the sense extra force is needed to get a mass moving. Remanence and stiction are both wrong and I'm not happy with drag. I expect the Greeks had a word for it! Dave
| |
| John Haine | 07/09/2023 19:16:49 | |
| 5563 forum posts 322 photos | "extra force is needed to get a mass moving"...inertia? | |
| Mike Everman | 07/09/2023 19:41:51 | |
| 3 forum posts | Some random comments: I tried the magnet/hoop thing and fringe effects dominated near the ends of the bar, as well as substantial eddy current damping, like imagine a Q of 2. Then, my simplistic EM drive was pulling on the steel of my bob, and through the data, I realized that the electromagnet was very slowly magnetizing the bob. Though the rate looked to be leveling off, it was in my tedious pre Microset days. I then just spent all my time on non-magnetic approaches, and have learned from recent experience that NdFeB magnets change quite radically with temperature. This drives you to conceptually flip everything over and look at the rod as a support instead of a tension member, as it all must translate in the direction of swing. If the bob is free to rotate, or more precisely, does not rotate with respect to ground, then every atom will follow the cycloid you've defined by whatever means. If it is rigid, all bets are off, and there is . As I recall, what killed the cheeks on Huygen's pendulum was the energy lost rotating a rigid bob and rod below the silk threads. I believe Alan Emmerson wrote a definitive proof of how a compound pendulum could never use cycloidal cheeks for isochronism. My takeaway from that was, "Oh, I just need to make a massless rod and a point mass. Simple!" | |
| Tony Jeffree | 07/09/2023 22:07:38 | |
569 forum posts 20 photos | Posted by Michael Gilligan on 07/09/2023 15:54:32:
Tony As you have so obviously got a grip on all of this … Would you please do me the favour of reading Huygens’ description of his layout process; and then explain exactly the result what he is doing ? Something in it doesn’t quite ring true The English translation of text is on the page that I posted
But, for everyone’s convenience, I will post the transcription of the Latin and IanBruce’s translation shortly. It all seems consistent in itself, but … MichaelG. Michael I certainly don't claim to have a grip on all of this! My observations above relate only to the discussion of the roller-with-attached-pendulum-suspended-under-a-(magnetic)-plane model - for that model to work you would (I believe) need the roller diameter to equal the effective pendulum length. The Huygens approach seems to be to use cycloidal cheeks - which reduce the pendulum's effective length as the amplitude increases. I've yet to try to get my head round why he chooses 1/2 the pendulum length to generate the curves for the cheeks. Regards, Tony | |
| duncan webster | 07/09/2023 22:58:08 | |
| 5307 forum posts 83 photos | It's covered in this article from Wikipedia. If it has stood the test of 300 years, and mathematicians such as Lagrange and Euler have been involved in providing proofs I think we can take it as read. To save flogging through it the significant sentence in my view is there were much more significant sources of timing errors that overwhelmed any theoretical improvements that traveling on the tautochrone curve helps. Finally, the "circular error" of a pendulum decreases as length of the swing decreases, so better clock escapements could greatly reduce this source of inaccuracy. In other words, keep the amplitude low and constant and forget about isochroism (if there is such a word) | |
| Mike Everman | 07/09/2023 23:31:24 | |
| 3 forum posts | Preaching to the choir and just getting my thoughts straight, but an isochronous approach would only be useful on a free pendulum. Making it less concerned about amplitude allows you to impulse it less often. A traditional escapement would need to unlock and impulse perfectly centered for it to benefit from this, right? | |
| david bennett 8 | 08/09/2023 01:11:46 | |
| 245 forum posts 19 photos | I don't think Huygens suggested that the cylinder had to be half pendulum size in diameter. It was just convenient. He was just using that to present his proof for his particular pendulum. Others since him have mis-interpreted his intentions.He wasn't trying to establish a rule for all cycloids, as we are. dave8 |
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - Winter Storage Of Locomotives
04/10/2023 21:02:11 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!










 Register
Register Log-in
Log-in


