diameter calculation
| Michael Gilligan | 13/10/2019 07:47:52 |
23121 forum posts 1360 photos | Posted by Jeff Dayman on 13/10/2019 00:34:16:
Agree Alan, it's getting ridiculous again, isn't it? Mind you, the egg cup I made this week was accurate to 22 millionths of an inch, and well worth the effort...... My goodness what a waste of time. The OP just wanted to know a shop grade calculation (and got one early on) . . Jeff, The question was answered, to the OP’s satisfaction, long ago. The discussion has evolved. Fact of Life ... That’s how it goes. Please give the whinging a rest. MichaelG. |
| Michael Gilligan | 13/10/2019 08:43:06 |
23121 forum posts 1360 photos | Posted by SillyOldDuffer on 12/10/2019 21:17:48:
. Oh dear […] . Dave, In deference to Mr Dayman’s sensitivities [*], I have sent you a personal message. MichaelG. [*] Sarcasm reared its ugly head in his post; so he’s obviously upset ! Edited By Michael Gilligan on 13/10/2019 08:50:41 |
| Nicholas Farr | 13/10/2019 09:07:32 |
3988 forum posts 1799 photos | Hi, yes, the question was answered to the OP's satisfaction, If one finds that the evolved thread becomes of no more interest to them, then they are not forced to read it any further, but of course it still interests others. Regards Nick.
|
| Hopper | 13/10/2019 09:56:19 |
7881 forum posts 397 photos | And we haven't even started to calculate how many angels can dance on the head of a pin of the diameter with three chords this size. I know the plain diameter formula has been posted on here before somewhere, but not encompassing the chords aspect. |
| Gary Wooding | 13/10/2019 10:38:21 |
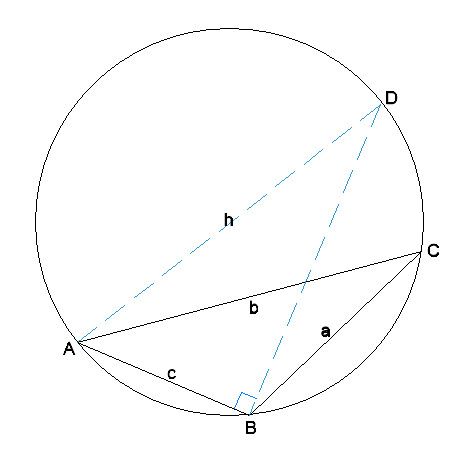
| 1074 forum posts 290 photos | Just to dot all the 'I's, here is my 'proof' of Nick's solution. It depends on two properties of chords in circles, and the Sine rule of trigonometry. 1. All angles subtended on one side by a chord to any point on the circumference are equal, so in the diagram, angle C equals angle D. 2. If the chord is a diameter, the angle is 90°, and conversely, if the angle subtended by a chord is 90° then the chord is a diameter. 3. The Sine rule states that, for any triangle, Sin A/a = Sin B/b = Sin C/c In the diagram, A, B, and C, are the three random points, and the circle is their PCD. You want to calculate the length of its diameter. Choose any side of the triangle ABC (side AB in the diagram) and draw a perpendicular line from one end to to meet the circle. This is the dashed line BD. Because they both come from chord AB, angles C and D are equal, so SinC = SinD. But SinD = c/h, so h = c/SinD = c/SinC But angle ABD is a right angle, so h = the diameter of the circle. |
| Nicholas Farr | 13/10/2019 18:14:19 |
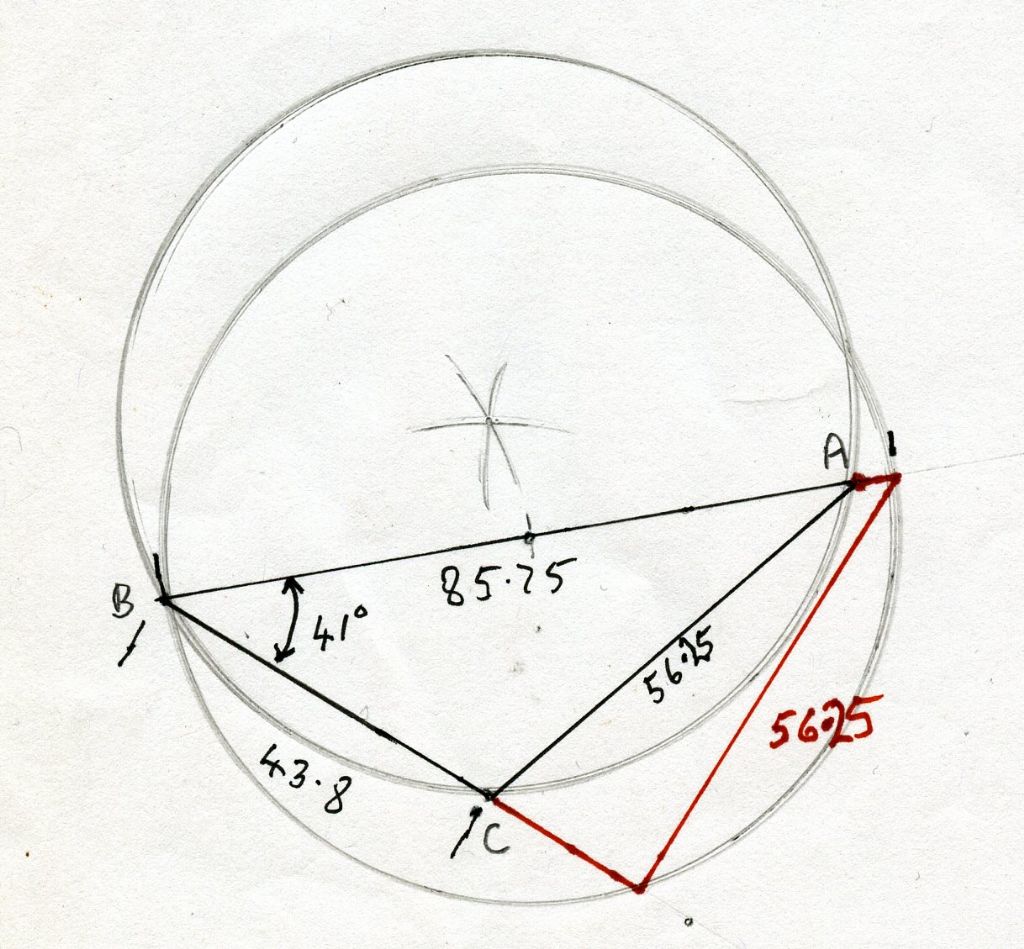
3988 forum posts 1799 photos | Hi Gary, a better way of proving the Sine rule works for the example 26 diagram is shown below. This is a half size one but the relationship between the angle and the length of the two sides shown are the same. This shows the integrity of the 41 degree angle and the lengths of the original sides and should help show those who don't quite understand how it works. The extended line B-A becomes the diameter of the PCD for A, B and C and a new PCD drawn on the centre of this line will show the Right Angle Triangle with the red line at a right angle to line B and C and it will be noticed that the new PCD will pick up both ends of the red line and point B. Excuse the makeshift real world drawing, all the dimensions are close to those actually calculated. Regards Nick. Edited By Nicholas Farr on 13/10/2019 18:18:25 |
| Andrew Johnston | 13/10/2019 18:43:24 |
7061 forum posts 719 photos | Posted by Neil Wyatt on 12/10/2019 19:10:29:
Actually there are LOTS of algorithms that produce answers by paying off accuracy against speed. I doubt they use algorithms in the sense of reaching a definitive answer without a full search, although probably in the sense that the sequence is gauranteed to halt. I suspect the answers are more likely based on heuristics. If Google has an algorithm that solves the travelling salesman problem then I expect they're in line for the Fields Medal. Andrew |
| Howard Lewis | 13/10/2019 21:35:36 |
| 7227 forum posts 21 photos | There's no hope for me! I could never work to better than two places with a 10" Faber Log-Log Slide rule. And now am WELL out of practice. (Still have it somewhere! ) Hopper did not specify the units of the diameter, or the tolerance thereof, of the head of the pin on which we have to have our angels dancing! Howard |
| Neil Wyatt | 13/10/2019 21:58:34 |
19226 forum posts 749 photos 86 articles | Posted by Andrew Johnston on 13/10/2019 18:43:24:
Posted by Neil Wyatt on 12/10/2019 19:10:29:
Actually there are LOTS of algorithms that produce answers by paying off accuracy against speed. I doubt they use algorithms in the sense of reaching a definitive answer without a full search, although probably in the sense that the sequence is gauranteed to halt. I suspect the answers are more likely based on heuristics. If Google has an algorithm that solves the travelling salesman problem then I expect they're in line for the Fields Medal. Andrew Solving it accurately isn't the issue, it's just the time taken. There are algorithms that speed things up, for example by calculating a near-optimal solution then testing alternatives based on it. The record for an accurate solution appears to be about 89,500 locations. en.wikipedia.org/wiki/Travelling_salesman_problem But there are LOTS of practical algorithms that trade absolute accuracy for huge increases in speed. |
| Neil Wyatt | 13/10/2019 22:00:32 |
19226 forum posts 749 photos 86 articles | Posted by Nicholas Farr on 13/10/2019 18:14:19:
Hi Gary, a better way of proving the Sine rule works for the example 26 diagram is shown below. This is a half size one but the relationship between the angle and the length of the two sides shown are the same. This shows the integrity of the 41 degree angle and the lengths of the original sides and should help show those who don't quite understand how it works. The extended line B-A becomes the diameter of the PCD for A, B and C and a new PCD drawn on the centre of this line will show the Right Angle Triangle with the red line at a right angle to line B and C and it will be noticed that the new PCD will pick up both ends of the red line and point B. Excuse the makeshift real world drawing, all the dimensions are close to those actually calculated. Regards Nick. Edited By Nicholas Farr on 13/10/2019 18:18:25 That's excellent & elegant. |
| Nicholas Farr | 13/10/2019 22:35:07 |
3988 forum posts 1799 photos | Hi Neil, thanks for your comment. The drawing is a bit rough and ready, but the 41 degree angle and the three points were set quite accurately and I think it shows what might seem to be an obscure triangle. Regards Nick.
|
| duncan webster | 13/10/2019 23:55:52 |
| 5307 forum posts 83 photos | Posted by Gary Wooding on 13/10/2019 10:38:21:
Just to dot all the 'I's, here is my 'proof' of Nick's solution. It depends on two properties of chords in circles, and the Sine rule of trigonometry. 1. All angles subtended on one side by a chord to any point on the circumference are equal, so in the diagram, angle C equals angle D. 2. If the chord is a diameter, the angle is 90°, and conversely, if the angle subtended by a chord is 90° then the chord is a diameter. 3. The Sine rule states that, for any triangle, Sin A/a = Sin B/b = Sin C/c In the diagram, A, B, and C, are the three random points, and the circle is their PCD. You want to calculate the length of its diameter. Choose any side of the triangle ABC (side AB in the diagram) and draw a perpendicular line from one end to to meet the circle. This is the dashed line BD. Because they both come from chord AB, angles C and D are equal, so SinC = SinD. But SinD = c/h, so h = c/SinD = c/SinC But angle ABD is a right angle, so h = the diameter of the circle. That's really elegant, but just to be pedantic, don't you need to use the cosine rule to find angle C to start the whole thing off rather than sin rule |
| SillyOldDuffer | 14/10/2019 10:09:03 |
| 10668 forum posts 2415 photos | Posted by Howard Lewis on 13/10/2019 21:35:36:
There's no hope for me! I could never work to better than two places with a 10" Faber Log-Log Slide rule. And now am WELL out of practice. (Still have it somewhere! ) Hopper did not specify the units of the diameter, or the tolerance thereof, of the head of the pin on which we have to have our angels dancing! Howard Oh dear, I seem to have stirred up a hornets nest by putting my foot in it again! For the record, my comments about extreme accuracy of calculation relate to the properties of Polar and Cartesian coordinates, not to Paul's original question. By asking about a practical problem, Paul opened the door to some interesting mathematical solutions and related problems. I questioned the assertion that Polar Coordinates are intrinsically more accurate than Cartesian Coordinates by suggesting both systems are equivalent provided the calculations are done to a sufficiently large number of decimal places. (Not convinced this is correct and Michael has set me some homework!) I wasn't suggesting Paul or anyone else needs to do hard sums in their workshops! The maths might seem obscure and irrelevant, but it's vital to engineering. For example, a variation of Andrew's 'Travelling Salesman Problem' has a workshop application. It's used to find the most economic way of cutting shapes from sheet material, important when stuff is stamped from metal, and very common issue in off-the-shelf tailoring. Micro-economies aren't worth the effort in a home workshop, but pennies matter hugely when millions are made. If maths is considered off-topic I apologise, but I've found value in all the posts, and don't mind at all that the conversation has opened out. Ta, Dave
|
| Michael Gilligan | 14/10/2019 15:02:46 |
23121 forum posts 1360 photos | Posted by SillyOldDuffer on 14/10/2019 10:09:03:
[…] For the record, my comments about extreme accuracy of calculation relate to the properties of Polar and Cartesian coordinates, not to Paul's original question. By asking about a practical problem, Paul opened the door to some interesting mathematical solutions and related problems. I questioned the assertion that Polar Coordinates are intrinsically more accurate than Cartesian Coordinates by suggesting both systems are equivalent provided the calculations are done to a sufficiently large number of decimal places. (Not convinced this is correct and Michael has set me some homework!) I wasn't suggesting Paul or anyone else needs to do hard sums in their workshops! […] . .
What I intended to assert was not that “Polar Coordinates are intrinsically more accurate than Cartesian Coordinates” But that ”for situations where Polar Coordinates properly specify the geometry, their use is intrinsically more accurate than a conversion to Cartesian Coordinates” ... It’s a subtle difference, but important. MichaelG. |
| SillyOldDuffer | 14/10/2019 16:46:52 |
| 10668 forum posts 2415 photos | Posted by Michael Gilligan on 14/10/2019 15:02:46:
Posted by SillyOldDuffer on 14/10/2019 10:09:03:
[…] For the record, my comments about extreme accuracy of calculation relate to the properties of Polar and Cartesian coordinates, not to Paul's original question. By asking about a practical problem, Paul opened the door to some interesting mathematical solutions and related problems. I questioned the assertion that Polar Coordinates are intrinsically more accurate than Cartesian Coordinates by suggesting both systems are equivalent provided the calculations are done to a sufficiently large number of decimal places. (Not convinced this is correct and Michael has set me some homework!) I wasn't suggesting Paul or anyone else needs to do hard sums in their workshops! […] . .
What I intended to assert was not that “Polar Coordinates are intrinsically more accurate than Cartesian Coordinates” But that ”for situations where Polar Coordinates properly specify the geometry, their use is intrinsically more accurate than a conversion to Cartesian Coordinates” ... It’s a subtle difference, but important. MichaelG. Arrgh! '... It’s a subtle difference, but important.' Certainly is. It's so easy to misread other people's posts! I am kicking myself...
Ta, Dave |
| Gary Wooding | 16/10/2019 12:18:37 |
| 1074 forum posts 290 photos | Posted by duncan webster on 13/10/2019 23:55:52:
........... but just to be pedantic, don't you need to use the cosine rule to find angle C to start the whole thing off rather than sin rule
Yes, you're right. |
| Chris Gunn | 17/10/2019 14:12:05 |
| 459 forum posts 28 photos | I am still struggling with the average of 1 and 2 being 2 Chris Gunn |
| Michael Gilligan | 17/10/2019 15:52:14 |
23121 forum posts 1360 photos | Posted by Chris Gunn on 17/10/2019 14:12:05:
I am still struggling with the average of 1 and 2 being 2 Chris Gunn . I think he rounded 1.5 up ... on the basis that 1 and 2 were expressed as integers. MichaelG.
|
| Chris Gunn | 17/10/2019 16:13:32 |
| 459 forum posts 28 photos | Thanks Michael, I knew I could rely on you. CG |
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - Winter Storage Of Locomotives
04/10/2023 21:02:11 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!










 Register
Register Log-in
Log-in


