Effect of Tensioning a Boring Bar
| SillyOldDuffer | 09/02/2020 16:44:45 |
| 10668 forum posts 2415 photos | Posted by Mick B1 on 09/02/2020 11:53:15:
Posted by SillyOldDuffer on 17/08/2017 17:29:14:
... Push rod hand tight - 2.25 seconds Push rod plus 1/2 turn - 1.41 seconds Push rod plus 1 turn - 1.35 seconds Push rod plus 1½ turns - 1.31 seconds Note the improvement isn't linear with increasing tension. ... I'm struggling to understand : i) how you can judge the cessation of visible vibes within a few hundredths of a second with a stoppwatch, or ii) that nobody else seems to've asked the same question Did I get bored and start to skip-read? Sometimes it's hard to tell... Averages, but otherwise guilty as charged...
Dave |
| John Paton 1 | 09/02/2020 21:09:36 |
327 forum posts 20 photos | maybe I am getting the wrong end of the stick, but ....... we have a tube to which we exert a lateral force at one end, resisted by compression of the steel on one side of it's neutral axis and stretching of the steel on the other side. steel stretches more than it compresses so by introducing some pretension the net effect will be to reduce bending. yes the increased stiffness wiLl alter the harmonic frequency but it is the reduction in deflection that we are really after. To me the logic of tension is sound but the margin of improvement is probably quite small.
Edited By John Paton 1 on 09/02/2020 21:11:20 |
| DrDave | 09/02/2020 21:20:32 |
| 264 forum posts 52 photos | Posted by John Paton 1 on 09/02/2020 21:09:36:
maybe I am getting the wrong end of the stick, but ....... we have a tube to which we exert a lateral force at one end, resisted by compression of the steel on one side of it's neutral axis and stretching of the steel on the other side. steel stretches more than it compresses so by introducing some pretension the net effect will be to reduce bending. yes the increased stiffness wiLl alter the harmonic frequency but it is the reduction in deflection that we are really after. To me the logic of tension is sound but the margin of improvement is probably quite small.
Edited By John Paton 1 on 09/02/2020 21:11:20 For a round bar, Engineer’s Theory of Bending tells us that the tensile and compressive stresses are the same. Preloading does not change the stiffness of the assembly. We need to look elsewhere for the reason that it can reduce chatter in a boring bar. |
| John Paton 1 | 09/02/2020 21:21:33 |
327 forum posts 20 photos | Thinking again' were the boring bar to be drilled along its length slightly to the rear of its centre and perhaps a shade below centre also a similar result may arise ( essentially trying to equalise compression on one side of the bar and extension on the other under given cutting forces) although this might not assist with torsional forces as well as preloading would. i am sure there are materials scientists in the group who can use real figures to quantify what I am trying (poorly) to get at. Doubtless the effect will vary greatly with different grades and temper of steel. |
| John Paton 1 | 09/02/2020 21:27:24 |
327 forum posts 20 photos | Posted by DrDave on 09/02/2020 21:20:32:
Posted by John Paton 1 on 09/02/2020 21:09:36:
maybe I am getting the wrong end of the stick, but ....... we have a tube to which we exert a lateral force at one end, resisted by compression of the steel on one side of it's neutral axis and stretching of the steel on the other side. steel stretches more than it compresses so by introducing some pretension the net effect will be to reduce bending. yes the increased stiffness wiLl alter the harmonic frequency but it is the reduction in deflection that we are really after. To me the logic of tension is sound but the margin of improvement is probably quite small.
Edited By John Paton 1 on 09/02/2020 21:11:20 For a round bar, Engineer’s Theory of Bending tells us that the tensile and compressive stresses are the same. Preloading does not change the stiffness of the assembly. We need to look elsewhere for the reason that it can reduce chatter in a boring bar. Is that still the case with something having a preload? I thought general black steel stretched more for a given force than it compressed (thinking back to materials lab days) but you may well be right and I will stand corrected. I confess that my experience with pretensioned components has always been with composite assemblies of dissimilar materials Deflection results from strain, does Young's modulus assume that the neutral axis is exactly central to a round bar? I had always assumed from work in the lab that under bending conditions the neutral axis wa slightly offset allowing compression and tensile forces to be equal despite the steel being stronger in compression than in tension. I am ready to learn on this as it is an aspect of materials science that is fascinating. Edited By John Paton 1 on 09/02/2020 21:34:30 |
| DrDave | 09/02/2020 21:32:12 |
| 264 forum posts 52 photos | Is that still the case with something having a preload? I thought general black steel stretched more for a given force than it compressed (thinking back to materials lab days) but you may well be right and I will stand corrected. Yes, unless you exceed the elastic limit (in tension or compression) for the boring bar material. But if you do, chatter is the least of your worries! |
| Michael Gilligan | 09/02/2020 21:54:07 |
23121 forum posts 1360 photos | Posted by DrDave on 09/02/2020 21:20:32:
[…]
Engineer’s Theory of Bending tells us that the tensile and compressive stresses are the same. Preloading does not change the stiffness of the assembly.
. Then could you please explain, in reasonably lay terms if possible, the findings in the report that I posted early this morning. Thanks MichaelG |
| DrDave | 09/02/2020 22:40:08 |
| 264 forum posts 52 photos | Posted by Michael Gilligan on 09/02/2020 21:54:07:
Posted by DrDave on 09/02/2020 21:20:32:
[…]
Engineer’s Theory of Bending tells us that the tensile and compressive stresses are the same. Preloading does not change the stiffness of the assembly.
. Then could you please explain, in reasonably lay terms if possible, the findings in the report that I posted early this morning. Thanks MichaelG A most interesting paper, MichaelG. The gist of it is to demonstrate the use of a high strength cable inside a structural steel section.. The steel cable is prestressed in tension, putting the tube into compression. Then, when an external tensile load is applied, the tube has to unload through zero and then start to pick up part of the applied load. The cable also picks up part of the applied load. The combination is much stronger than the tube on its own, when loaded to failure. I guess that the prestressed tube is lighter than just using a bigger tube without prestress. One thing I hadn’t realised is the support provided by the cable increases the Euler buckling strength of the tube. Clever! So, prestressing a low-strength tube is an effective method of increasing the ultimate tensile strength of the member. I cannot see, however, any correlation with vibration in a boring bar. Dave |
| Michael Gilligan | 09/02/2020 22:57:38 |
23121 forum posts 1360 photos | Thanks for the prompt reply, Dave I was with you right up to the end of your penultimate sentence ... and then I realised that we must be seeing this very differently. I’ll sleep on it. MichaelG. |
| John Paton 1 | 09/02/2020 23:08:21 |
327 forum posts 20 photos | Posted by DrDave on 09/02/2020 21:32:12:
Is that still the case with something having a preload? I thought general black steel stretched more for a given force than it compressed (thinking back to materials lab days) but you may well be right and I will stand corrected. Yes, unless you exceed the elastic limit (in tension or compression) for the boring bar material. But if you do, chatter is the least of your worries! Got it - thanks DrD! |
| Michael Gilligan | 09/02/2020 23:27:12 |
23121 forum posts 1360 photos | Posted by DrDave on 09/02/2020 21:20:32:
[…]
For a round bar, Engineer’s Theory of Bending tells us that the tensile and compressive stresses are the same.
. I was a little nervous when I first read that assertion ... so I tried some self-help and found this; which I think is what’s known as Engineer’s Theory of Bending: **LINK** http://www.idc-online.com/technical_references/pdfs/mechanical_engineering/Simple_Bending_Theory.pdf If so, I must mention that what it “tells us” appears to actually be one of its several assumptions. Do please correct me if I have found the wrong theory. MichaelG.
|
| duncan webster | 10/02/2020 12:26:25 |
| 5307 forum posts 83 photos | I was going to let this run and not have any more input, but recent posts have brought in several misconceptions. Apologies to those who are already up to speed, but some basic definitions will not be out of place. Some of this has been said before in this thread, but will stand repetition. Strength and stiffness are not the same thing. Strength is the ability of a material to support a load without taking on a permanent deformation (Yield Stress) or without breaking (Ultimate Tensile Stress). Stiffness is the relationship of load to extension within the elastic range. These are plainly not the same. As we are most unlikely to load a steel boring bar to the point where it takes on a permanent bend, we can concentrate on stiffness. To quote Raymond J Roark (Professor of Mechanics, Wisconsin University): Modulus of elasticity (Young’s Modulus):- The rate of change of unit tensile or compressive stress with respect to unit tensile or compressive strain for the condition of uniaxial stress within the proportional limit. For most, but not all materials the modulus of elasticity is the same for tension and compression…….(page 9 4th edition, Formulas for Stress and Strain) For steel, Young’s modulus is pretty much a straight line until the stress reaches the limit of proportionality. This is not far below the elastic limit (Yield Stress), so need not trouble us further. Soft materials (annealed copper, lead, zinc etc) have a curved relationship. Grey cast iron has flakes of graphite in its structure which allow the material to ‘gape’ under tension, so its Young’s modulus is tension is lower than that in compression. Then on page 23 Roark states: All steels have the same E (Young’s modulus), K (bulk modulus) and G (shear modulus), these quantities being but little affected by composition or heat treatment. This last isn’t quite correct, stainless steel is about 25% not iron, and has a slightly lower Young’s modulus (in the range 190/203 MN/m^2) compared with 207 for non stainless), but changing from EN3 to EN8 won't make any difference to stiffness. For an explanation of all this in layman’s terms I recommend 2 books by J.E Gordon, Structures, or why things don’t fall down, and The new science of strong materials, or why we don’t fall through the floor. These should be required reading for engineering students. Roark’s book is the bible of stress calculation, my paper copy is ancient, I think it is up to at least edition 8, and has been revised by Warren C Young and Richard G Budynas, both professors at US universities (and made less understandable in the process). I have 7th edition as a pdf, but it's probably copywright. |
| Graham Meek | 10/02/2020 12:51:16 |
| 714 forum posts 414 photos |
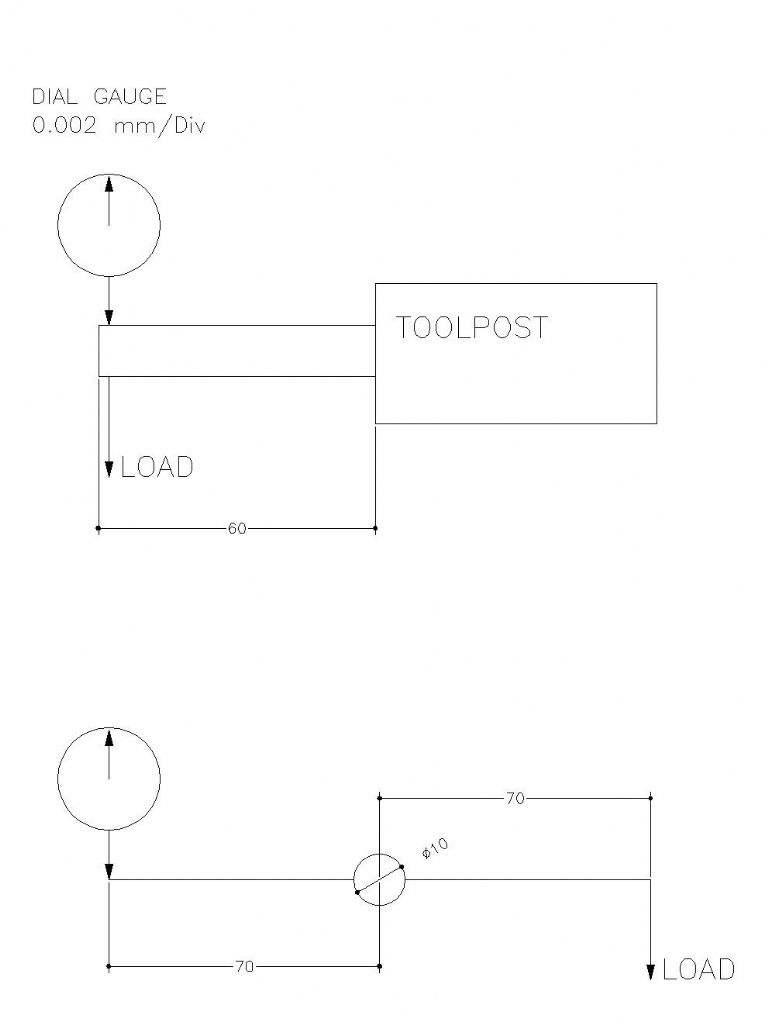
I am convinced the Boring bar problem cannot be treated as simple Bending Theory alone. There are several forces going on at the same time. Thus this morning I have carried out a few tests. The diagram above gives the outline of the two tests I carried out. One is testing the deflection of the Boring bar under load. The other is testing the boring bar in torsion. A standard deflection was chosen to simplify things and 10 results were obtained for each test. In the first test it took an average of 3.85 kg to deflect a Plain bar 0.05 mm, (0.002" approx). While the boring bar under a pre-tension took 4.53 kg to deflect the same 0.05 mm. An improvement of 15%. In the Torque test the plain bar took 1.13 kg to deflect the arm 0.05 mm, while the boring bar under a pre-tension took 1.59 kg. This time there was a much bigger improvement of 30%. These test were purposely carried out with above normal projection from the Toolpost and one would hardly have a tool tip 70 mm from the centreline, but I do think this does help to quantify what is happening. It is obvious to me the improvement under torsion is the key to the success I had in my initial post on the matter. The tool twisting in and out of the cut is what starts off the oscillations which causes the chatter. Regards Gray, Edited By Graham Meek on 10/02/2020 12:53:22 |
| Martin Kyte | 10/02/2020 13:02:19 |
3445 forum posts 62 photos | So now we have established that the bar is not going to be any any stiffer and building a rod within a tube can only make it less so. and chatter is a sustained oscillation which by definition must be a resonance then the likely candidate for Graham Meeks' observed improvement in performance has to be either a shift in the resonant frequency or at least a change in the frequency response to make it less 'tuned'. After all a simple round bar held by it's end is a better candidate to go 'twang' than a composite arrangement of a rod within a tube which I can imagine to be more of a 'thunk' than a 'twang'. regards Martin |
| Michael Gilligan | 10/02/2020 17:11:15 |
23121 forum posts 1360 photos | Posted by Martin Kyte on 10/02/2020 13:02:19:
So now we have established that the bar is not going to be any any stiffer and building a rod within a tube can only make it less so. […] .
My reading of Graham Meek’s simple practical test results indicates quite the contrary !! [quote] In the Torque test the plain bar took 1.13 kg to deflect the arm 0.05 mm, while the boring bar under a pre-tension took 1.59 kg. This time there was a much bigger improvement of 30%. [/quote] MichaelG. . P.S. I can claim no expertise in stress analysis ... but I did work for eleven years in an Environmental Test House, and have done some serious vibration testing.
Edited By Michael Gilligan on 10/02/2020 17:15:32 |
| DrDave | 10/02/2020 18:58:27 |
| 264 forum posts 52 photos | Posted by Graham Meek on 10/02/2020 12:51:16:
In the first test it took an average of 3.85 kg to deflect a Plain bar 0.05 mm, (0.002" approx). While the boring bar under a pre-tension took 4.53 kg to deflect the same 0.05 mm. An improvement of 15%. In the Torque test the plain bar took 1.13 kg to deflect the arm 0.05 mm, while the boring bar under a pre-tension took 1.59 kg. This time there was a much bigger improvement of 30%. Graham, can you let me know whether the “plain bar” was a simple, solid bar, or whether its was the “bar within a tube” boring bar that you did the pretensioned tests on? Ta Dave |
| DrDave | 10/02/2020 19:58:04 |
| 264 forum posts 52 photos | Posted by Michael Gilligan on 09/02/2020 23:27:12:
Posted by DrDave on 09/02/2020 21:20:32:
[…]
For a round bar, Engineer’s Theory of Bending tells us that the tensile and compressive stresses are the same.
. I was a little nervous when I first read that assertion ... so I tried some self-help and found this; which I think is what’s known as Engineer’s Theory of Bending: **LINK** http://www.idc-online.com/technical_references/pdfs/mechanical_engineering/Simple_Bending_Theory.pdf
Yes, that is what I had in mind with Engineer’s Theory of Bending: my apologies for using jargon. Duncan explained it rather well, above. Dave |
| Michael Gilligan | 10/02/2020 20:26:22 |
23121 forum posts 1360 photos | Thanks, Dave I do note however that you omitted [inadvertently ?] my observation that: If so, I must mention that what it “tells us” appears to actually be one of its several assumptions. . i.e. ... The “theory” is a simplified method of calculation, based on several convenient assumptions. Several aspects of our ‘hollow beam with pushrod’ are precluded by those assumptions, so I would submit that it is inappropriate for the detailed analysis that we need to apply. As I hinted earlier: I think we need to see some decent Finite Element Analysis. MichaelG. . . Here’s a mesh that Mark created for an ER collet holder, before he left the forum:
Edited By Michael Gilligan on 10/02/2020 20:33:13 |
| DrDave | 10/02/2020 20:32:11 |
| 264 forum posts 52 photos | Posted by Michael Gilligan on 10/02/2020 20:26:22:
Thanks, Dave I do note however that you omitted [inadvertently ?] my observation that: If so, I must mention that what it “tells us” appears to actually be one of its several assumptions. (...) As I hinted earlier: I think we need to see some decent Finite Element Analysis. MichaelG. I was hoping that you would not spot that... I tried doing the maths for a two-spring system, but it never was my strong subject so I gave that up. I will try to round up some fine white elephants at work tomorrow and see if that answers any questions, or just gives more of them! Dave |
| Martin Kyte | 11/02/2020 08:48:18 |
3445 forum posts 62 photos | Posted by Michael Gilligan on 10/02/2020 17:11:15:
Posted by Martin Kyte on 10/02/2020 13:02:19:
So now we have established that the bar is not going to be any any stiffer and building a rod within a tube can only make it less so. […] .
My reading of Graham Meek’s simple practical test results indicates quite the contrary !! [quote] In the Torque test the plain bar took 1.13 kg to deflect the arm 0.05 mm, while the boring bar under a pre-tension took 1.59 kg. This time there was a much bigger improvement of 30%. [/quote] MichaelG. . P.S. I can claim no expertise in stress analysis ... but I did work for eleven years in an Environmental Test House, and have done some serious vibration testing.
Edited By Michael Gilligan on 10/02/2020 17:15:32
To be fair, Graham posted that whilst I was writing my bit so I had not read it. My point was that using the same materials, a rod within a rod not under tension,(but not loose) cannot be intrinsically stiffer. So either the bar cannot be modelled by simple linear spring theory or it's a harmonic phenomena. It does undoubtably practically work, as Graham has shown. I look forwards to someone moving this forward, it is quite interesting. regards Martin
|
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - Winter Storage Of Locomotives
04/10/2023 21:02:11 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!











 Register
Register Log-in
Log-in


