JoNo's Pendulum
| duncan webster | 31/08/2023 13:33:40 |
| 5307 forum posts 83 photos | To quote JFK, because it's hard. It keeps the grey cells going, both those who are actually doing it, and we who merely look on in awe. |
| Joseph Noci 1 | 31/08/2023 18:25:40 |
| 1323 forum posts 1431 photos | Its making my grey cells grey.. I have difficulty in coming to grasps with this : if the pendulum amplitude is kept truly constant, what does the period do if the pendulum rod grows in length? |
| S K | 31/08/2023 19:13:06 |
| 288 forum posts 42 photos | Posted by Joseph Noci 1 on 31/08/2023 18:25:40:
Its making my grey cells grey.. I have difficulty in coming to grasps with this : if the pendulum amplitude is kept truly constant, what does the period do if the pendulum rod grows in length? It depends on where and how you are measuring the amplitude, doesn't it? If you are using an angular sensor at the top, then it doesn't know anything about the length, and if the length of the rod grows, the pendulum will slow down. If you are measuring the amplitude as the peak swing in X at the bottom, then longer length also means slower. To do this properly, the sensor for this should travel along with the pendulum, e.g. instrumented on a dummy pendulum. But most have the sensors mounted to the pendulum's support, which will typically shift in space independently of the pendulum itself as the temperature changes. Even the placement of the sensors in X matters. John measured 1um position resolution of his opto. But almost any support fixing the opto's position will shift that much with a one degree change in temperature. Edited By S K on 31/08/2023 19:21:05 |
| Michael Gilligan | 31/08/2023 19:16:45 |
23121 forum posts 1360 photos | Intuitively, I would say the pendulum would swing more slowly … but that probably depends on how you are measuring ‘amplitude’ i.e. whether the notion of ‘truly constant amplitude’ refers to the angle swung, or to the maximum linear excursion of some nominal point which [say] triggers a light trap. I’m struggling here … but I think the answers would be different. MichaelG.
|
| duncan webster | 31/08/2023 21:40:41 |
| 5307 forum posts 83 photos | Longer pendulum is longer period for the same angular swing. If you're controlling distance rather than angle, then longer pendulum is lower angle, and lower angle gives longer period in its own right. I think the effect of longer pendulum is dominant, but am open to correction Edited By duncan webster on 31/08/2023 21:42:29 Edited By duncan webster on 31/08/2023 21:43:42 |
| Martin Kyte | 31/08/2023 23:24:48 |
3445 forum posts 62 photos | M H Robert’s table in Precision Pendulum Clocks shows a loss of 1.05. mins in 24 hours at 6 degrees amplitude which falls to 14.8 secs in 24 hours at 3 degrees which to my understanding demonstrates that the period increases with amplitude. regards Martin Edited By Martin Kyte on 31/08/2023 23:25:48 |
| duncan webster | 01/09/2023 00:17:53 |
| 5307 forum posts 83 photos | Martin, you're correct, looks as if I've remembered it incorrectly. This gives the expression for a large amplitude pendulum, and shows that period goes up as angular amplitude goes up. If I can't think of anything better to do I'll try to add the effect of length increasing to angular amplitude decreasing for a fixed distance amplitude, but that will have to wait until tomorrow |
| Joseph Noci 1 | 01/09/2023 00:30:03 |
| 1323 forum posts 1431 photos | The formulae for pend. period shows directly that period increases with length, but I am trying to understand what happens if angular displacement is kept constant all the time. When the length , or radius, increases, the distance the bob swings ( the arc length) increases for the same displacement angle. Since I am controlling displacement angle and not rate, I guess the rate must reduce.. Its nearly 2 in the morning... |
| duncan webster | 01/09/2023 00:43:51 |
| 5307 forum posts 83 photos | Yes, if you're controlling angle of swing, and the pendulum gets longer, the period increases. I've just realised that using optical methods on either the bob or a vane, and the edge which does the interrupting is parallel to the rod, changing the pendulum length shouldn't make any difference, you are actually measuring angle. Won't work with a spherical or other funny shape if the bob is doing the interrupting Edited By duncan webster on 01/09/2023 00:46:08 |
| John Haine | 01/09/2023 06:57:27 |
| 5563 forum posts 322 photos |
No, I mean log amplitude but linear time. For each cycle take its peak, normalise to the starting amplitude, then take the log. The resulting value for pure exponential decay will be a straight line with negative slope. |
| John Haine | 01/09/2023 07:15:30 |
| 5563 forum posts 322 photos | Posted by Joseph Noci 1 on 31/08/2023 08:10:22:
Posted by John Haine on 31/08/2023 07:14:37:
... After many hours of running and adjusting the weights I have it reasonably stable @ 0.5Hz with a 100us or so jitter. However, simply opening a 800mmx300mm cupboard door, 3 meters from the pendulum, causes a 3-400us jump within 1/2 a second of opening the door. The pendulum is in the study ( 2nd storey of the house..), on a thick concrete floor, but walking slowly on the floor 1 meter from the pendulum causes a similar jump - maybe motion, maybe air movement, or both. Also, I have the Atlantic ocean crashing 50 meters from the house...Perhaps Fishing would be a more successful pastime? Joe, you are in a unique position to repeat an experiment that has only been done once! You have a pendulum in a location with regular seismic noise which is, uniquely, properly instrumented to measure its motion. Many years ago Doug Bateman noticed that the pendulum of his clock had a tiny motion even when not having been impulsed. This seemed to be due to vibration of the support point. Doug made measurements using a travelling microscope. Philip Woodward analysed the motion of a pendulum subject to random motion of the support with an important conclusion, that the main cause of error was small random changes in amplitude via circular deviation, and the effect of this increases with Q! This is unlike errors caused by internal impulse noise which are reduced by higher Q. Other than Doug's observations, to my knowledge the only other observation has been by Bryan Mumford (of the Microset) who logs the timekeeping of the courthouse clock in Santa Barbara. He saw a large transient in the period caused by an earthquake in California, and based on that a lot of horologists argue that high Q is undesirable, but no one has done proper measurements. So it would be really interesting to just turn off the impulsing, let the pendulum coast down, and log the remaining motion for as long as convenient, if the SNR of your angle sensor permits. No need for very rapid sampling either, the bandwidth of the motion is a fraction of a hertz. |
| Joseph Noci 1 | 01/09/2023 20:55:00 |
| 1323 forum posts 1431 photos | Posted by John Haine on 01/09/2023 06:57:27:
Posted by Joseph Noci 1 on 31/08/2023 09:12:55:
John, Is this 'log' plot format what you mean?
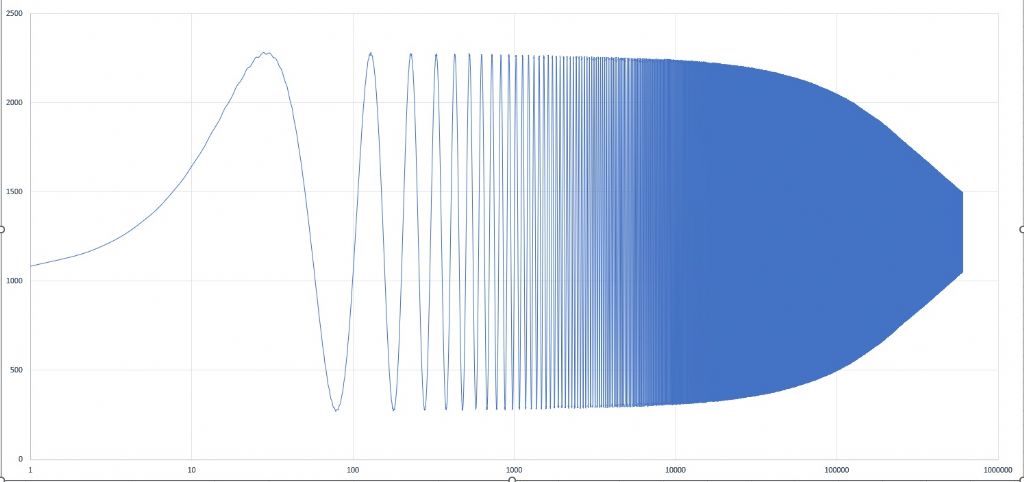
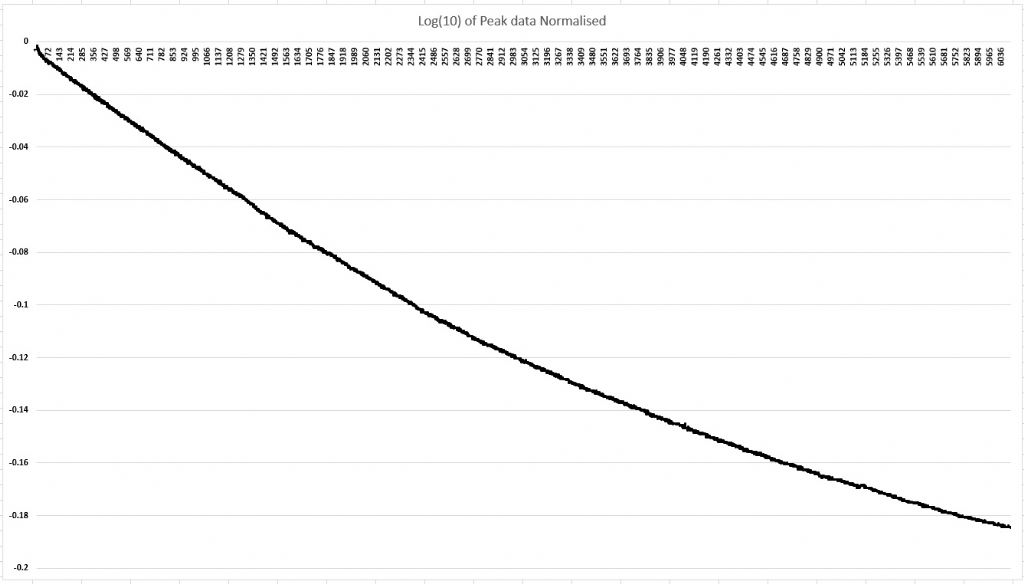
No, I mean log amplitude but linear time. For each cycle take its peak, normalise to the starting amplitude, then take the log. The resulting value for pure exponential decay will be a straight line with negative slope. Ok, I think I have plotted it correctly - This is a plot of Log(10) of normalised data: Not exactly a straight line.
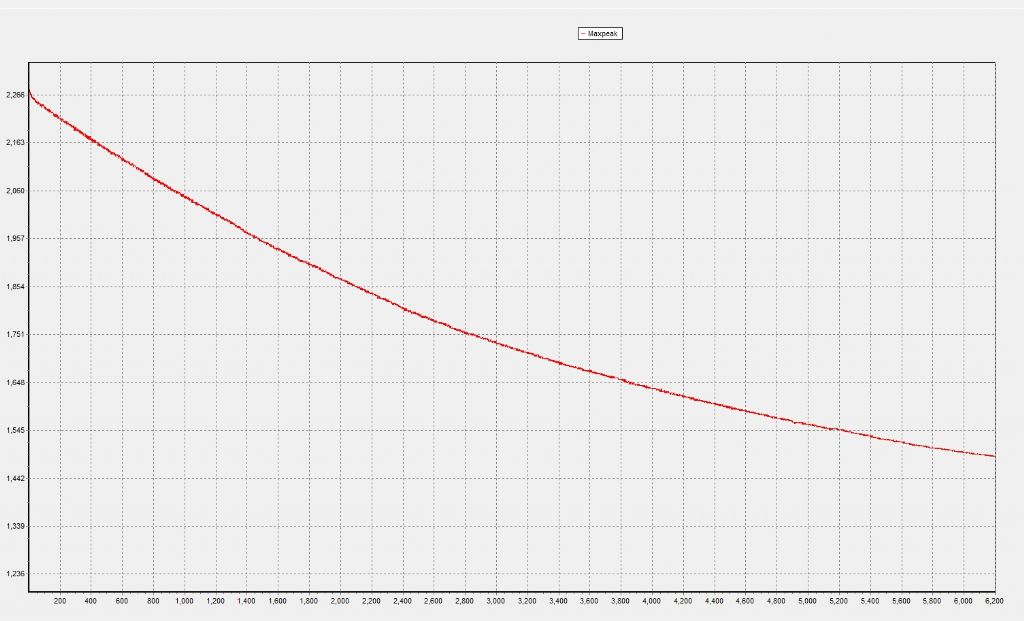
This is a plot of just the peak values - extracted from the Angle sensor output file, with peaks extracted These plots are are the same for all intents... What am I missing?
John, you also said - You plot the decay I think on a linear amplitude scale. It would be interesting to plot it on a log (ln) scale which is more natural for exponential decay. But it's fairly clear that there is a "break point" where the slope decreases. If you are seeing essentially an exponential shape it's a good indication that the loss is primarily aerodynamic - other forms of loss give different shapes. My pendulum test showed exactly such a break point, with a somewhat higher Q for that part of the decay above it. Where do you see the break point - in which curves? I would like to understand better. Also, which curve am I looking at to see 'essentially an exponential shape' ? The Log plot, or my straight amplitude decay curve? I am somewhat confused - As my log plot is not a straight line, does this imply that my losses are primarily NOT aerodynamic? If so, the the losses must lie in the pivot? Or should the curve BE exponential confirming a 'good' set of mechanics, with losses mainly aerodynamic? I am not sure if what I have is good or bad, nor the reason why! |
| Michael Gilligan | 01/09/2023 21:34:21 |
23121 forum posts 1360 photos | I am very rusty on this stuff, Jo … but I think you might want to use the natural logarithm: https://youtu.be/mUfXkwTQB8o?feature=shared This looks like a good tutorial … I’m off to get a drop of Jura MichaelG. . Edit: __ Try here: https://serc.carleton.edu/sp/library/teachingwdata/graphsexponential.html Edited By Michael Gilligan on 01/09/2023 22:06:39 |
| Michael Gilligan | 01/09/2023 22:08:22 |
23121 forum posts 1360 photos | Too late to re-edit that untidy post MichaelG. |
| John Haine | 01/09/2023 22:15:05 |
| 5563 forum posts 322 photos | The natural log will just have the same numbers multiplied by a constant, which from memory is I think 2.302 [ln(10)] (could be wrong). Joe, could you email me the numbers behind one of the plots please? I could try to illustrate what I mean. |
| Joseph Noci 1 | 01/09/2023 23:38:46 |
| 1323 forum posts 1431 photos | John, I have emailed the angle sensor file to you - it is the one from my last Q run - Sensor sine wave output in millivolts. I changed the lateral pivots this afternoon - from the pin in V groove to pin on a hard steel flat - WIll post photos for your comments please. Did a Q run again, in prep for the 'remaining motion' test, and the Q is below 8000! So I am investigating where the new friction comes from - did not touch the knife edge setup, but fast believing the knife edge is difficult to set up properly. It is not easy to get the knife edges perfectly at right angles to the swing plane - even lying in the trough of the bearing inner race, the knife can move forward 0.1/0.2mm on one side while the other stays where it is and then the knife pivots across non aligned edges - hard to describe but alignment is a big issue. I will do your test once my Q values are back... |
| S K | 02/09/2023 09:50:12 |
| 288 forum posts 42 photos | About alignment: Your effort is amazing, but I was surprised to see you have the square knife edge riding on an inside circular surface. All knife-edge setups I've seen have a knife or knives riding on one or two flat surface(s), or vice versa (as in my previous version, which was flats on knives). Your setup makes theoretical sense, but I feel like your square shank could easily find itself miss-positioned, riding up higher than absolute bottom dead center on either or both sides (I think you have two pivots, right?), or skewed between the sides. Especially in the latter circumstance, I could imagine friction going up. You just changed from V's to flats on the other axis, so why round for your primary one? Also, using two quite hard steel surfaces (your knife and your inner race) sounds good, but if they are close to each other in hardness, one will inevitably bite into the other. I used sapphire for the flat surfaces, and the steel knives just won't scratch it (dulling of the knives certainly can still happen, but I never got around to polishing their edges anyway). On a different but related point, my limited experience leads me to feel that my new spring-hinge mounted pendulum is considerably more susceptible to wobble than my old knife-edge pendulum. In the latter case, the main source of wobble was flexibility of the rod (aside from obvious lifting off of the knife-anvil interface when ham-handling it), whereas the spring hinge can easily permit a certain amount of wobble by itself in addition to the rod flexing. I've felt like the spring hinge was a step backward. Finally, something that I, at least, have been guilty of many times: presuming that this or that technique should and hence must yield superior results, followed by bafflement when it doesn't pan out. That's when the gods really start chuckling. 😉 Edited By S K on 02/09/2023 10:05:36 |
| Joseph Noci 1 | 02/09/2023 11:48:37 |
| 1323 forum posts 1431 photos | Unfortunately its not that simple - The knife riding in the curve is intentional as the capacitive angle sensor vane has to rotate around the pendulum pivot point, which is the knife contact edge. The sensor registers and van movement, which in my case must only be rotation around the pivot. Any movement of the knife on its ledge inthe swing direction is therefore a movement of the vane, indiscernible from movement due to rotation, so it registers and offset, ie, the angle sensor peak to peak measurement remains a constant, but the midpoint is offset by the amount the knife is moved. The knife in the bearing inner race trough is an attempt to make it always sit at the lowest point, but not accurate enough. I don't like the springs - esp two springs separated as appears to be the norm - if the annealing of both is not identical ( esp if brazed, etc), or the length of each differs slightly, or the clamp zone contact points are not the same, etc, one spring bends more than its mate, and the rod twists.... |
| duncan webster | 02/09/2023 11:57:36 |
| 5307 forum posts 83 photos | Many moons ago there was a description of a clock in ME where the pivot was a Stanley knife blade rocking on a piece of tungsten carbide. The carbide had a scratch to encourage the knife not to go walkies. A suggested improvement was to put the blade facing upwards, fixed to the support, and the carbide on the pendulum facing down in a sort of inverted stirrup arrangement. This was to stop it collecting dust |
| SillyOldDuffer | 02/09/2023 12:00:38 |
| 10668 forum posts 2415 photos | Posted by Michael Gilligan on 01/09/2023 21:34:21:
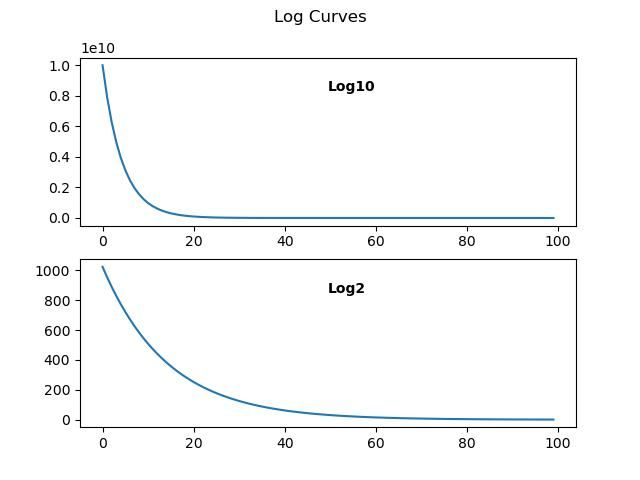
I am very rusty on this stuff, Jo … but I think you might want to use the natural logarithm: ...MichaelG. Not only am I rusty, but I was never smart in the first place! And my maths is dreadful. However, I'm happy to my have my thoughts marked out of ten. Could be embarrassing! As I understand it, at this stage, the base of the logarithm doesn't matter. The shape of a logarithmic curve on a graph is representative of exponential decay, which is typical of energy being lost from a closed system. Joe's graph looks to have a curve characteristic of exponential decay, but we don't know what the exponent is. Examples of exponential curves: Point here is that Log Base 10 and Log Base 2 have the same basic shape, as does Joe's curve, except his could be log base 1.2 or something else. An exponential curve is one where a power is present in the equation that describes the curve. Powers less than 1 are roots. (√4 is 4 to the power 0.5) If taking the log of a graphed curve tends to straighten it, then that's evidence the curve is exponential. Many phenomena result in a straight-line graph. Many others produce curves and this class includes energy loss. A generator or chuck running down when power to the motor is cut, a bouncing ball, pressure falling in a emptying water-tank, mechanical oscillators overcoming friction, or electronic oscillators overcoming electrical resistance all produce exponential decay curves. After a ball is dropped from a height it rebounds less and less on each bounce. If the rebound height is graphed per bounce, the curve will be found to decay exponentially. The energy loss on each bounce is non-linear. The value of the exponent depends on the mechanical nature of the floor and ball, and air resistance and can be calculated in various ways, such the least squares method. To my mind knowing the exponent's value isn't all that useful, because for pendulista purposes it provides much the same information as Q. However, it's important to ensure that a pendulum's decay curve really is exponential because the Q calculation depends on it! I'd bet the farm that Joe's curve is exponential, but think it's a step too far to assume that's proof of aerodynamic resistance. Even though aerodynamic resistance is highly likely to be a major player. Fanning air is a major cause of energy loss in a pendulum, even if the bob is aerodynamically efficient. Dave
|
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - Winter Storage Of Locomotives
04/10/2023 21:02:11 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!










 Register
Register Log-in
Log-in


