Pendulum 'Q' value and measurement methods
| S K | 18/08/2023 01:15:27 |
| 288 forum posts 42 photos | If I estimate your "half power bandwidth" to be 2 times your standard deviation (that's the number I have, anyway), then after rounding the numbers for simplicity, I get Q=1/(2*0.001)=500. How do you get over 20,000? What numbers do you have? Also, you expressed concern about how your cumulative time error had wandered. This is due in large part to the accumulation of many small random errors in a classic random walk. If those small errors are 250 times lower (i.e., S.D. = 4us vs. 1ms), then the cumulative deviations should, in an typical run, also be 250 times lower. So yes, you do want as low a standard deviation as you can get. Edited By S K on 18/08/2023 01:46:06 |
| Michael Gilligan | 18/08/2023 06:52:37 |
23121 forum posts 1360 photos | This might be useful: **LINK** http://www.vibrationdata.com/tutorials2/half_power_bandwidth.pdf It’s a long while since I worked in vibration testing, but it looks right. caveat lector MichaelG. |
| John Haine | 18/08/2023 11:05:14 |
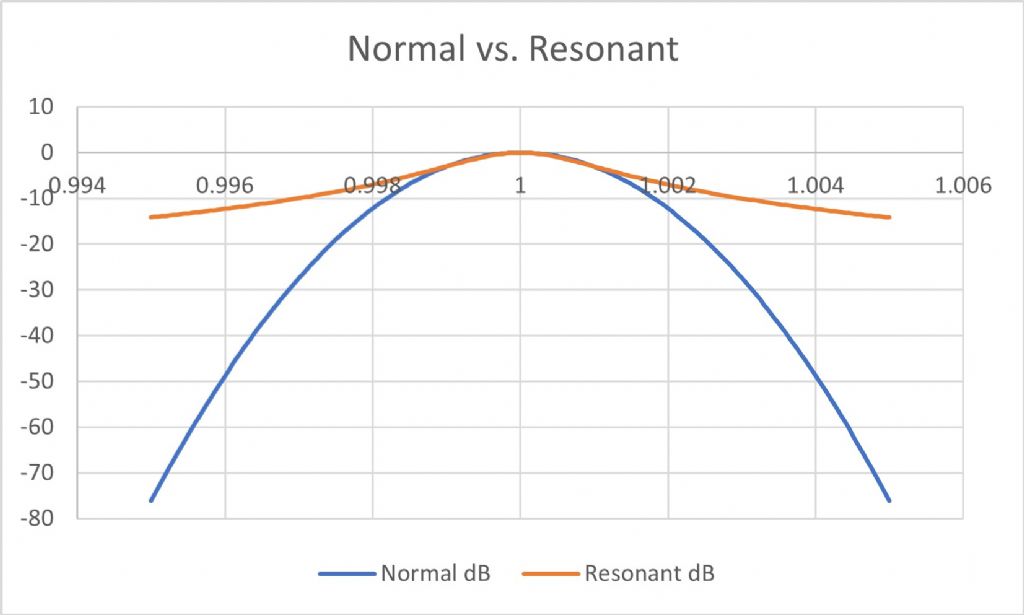
| 5563 forum posts 322 photos | I thought it would be interesting to directly compare the normal distribution curve with a resonance curve according to the equation Dave quoted above. In this picture the normal (blue) curve is plotted using Excel's normal distribution function normalised so the peak is unity. I've normalised the mean to unity and the standard deviation to the value that Dave measured divided by his period, to give 0.001194. I've plotted the vertical axis in dB to make it easy to compare the 3dB points. I wasn't quite sure how to render the vertical probability axis in dB since it doesn't really have a meaning but I chose 20*log10 to match what I did with the resonance formula. The resonance curve (orange) used the same centre frequency of 1Hz and I twiddled the Q to to get the -3dB points to match the normal curve, which needed a Q of ~500. What's obvious is that though the curves are similar around the peak they diverge hugely as one moves away, by 10s of dB. It seems to me that the period error must depend on the Q, obviously, but also on the "noisiness" of the whole oscillator, and the amplitude of the oscillation which the noise is perturbing. Those factors are captured in the equation I posted. Clock B is a nice example - the pendulum has a rather low Q compared to most regulators, but it swings with about 4 - 6x the amplitude, the drive torque is very accurately controlled with a remontoire, the escapement minimises frictional variation of force, the whole thing is extremely massive and (for the critical tests) was mounted on a masonry column embedded in boulder clay; and finally the pendulum is temperature and barometrically compensated. I think Dave's distribution looks very gaussian (normal) and is actually a very useful measure though not of Q! It tells us I think that the systematic variations are pretty small and most of the fluctuations are random, though they could be due either to the oscillator or the measurement system. |
| SillyOldDuffer | 18/08/2023 17:44:37 |
| 10668 forum posts 2415 photos | Posted by John Haine on 18/08/2023 11:05:14:
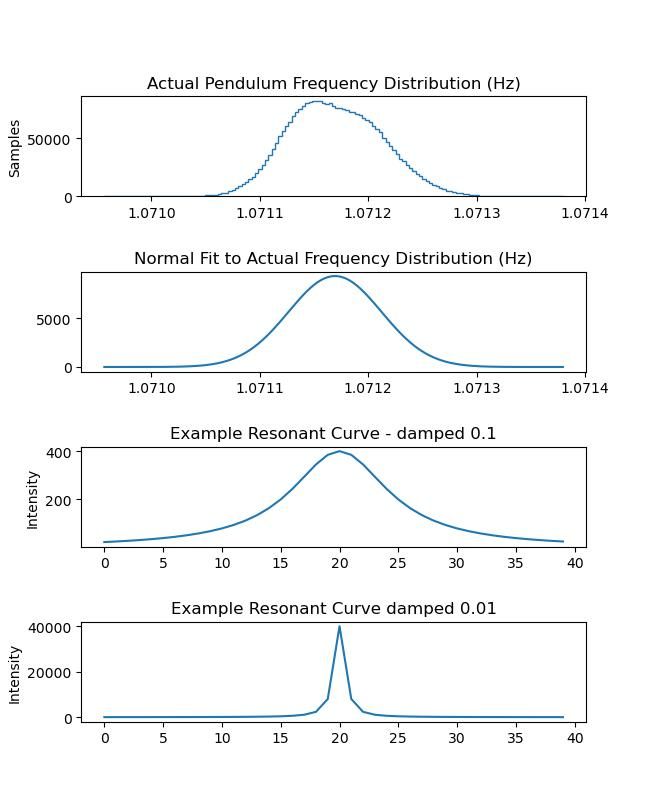
I thought it would be interesting to directly compare the normal distribution curve with a resonance curve according to the equation Dave quoted above. In this picture the normal (blue) curve is plotted using Excel's normal distribution function normalised so the peak is unity. I've normalised the mean to unity and the standard deviation to the value that Dave measured divided by his period, to give 0.001194. I've plotted the vertical axis in dB to make it easy to compare the 3dB points. I wasn't quite sure how to render the vertical probability axis in dB since it doesn't really have a meaning but I chose 20*log10 to match what I did with the resonance formula. The resonance curve (orange) used the same centre frequency of 1Hz and I twiddled the Q to to get the -3dB points to match the normal curve, which needed a Q of ~500. What's obvious is that though the curves are similar around the peak they diverge hugely as one moves away, by 10s of dB. It seems to me that the period error must depend on the Q, obviously, but also on the "noisiness" of the whole oscillator, and the amplitude of the oscillation which the noise is perturbing. Those factors are captured in the equation I posted. Clock B is a nice example - the pendulum has a rather low Q compared to most regulators, but it swings with about 4 - 6x the amplitude, the drive torque is very accurately controlled with a remontoire, the escapement minimises frictional variation of force, the whole thing is extremely massive and (for the critical tests) was mounted on a masonry column embedded in boulder clay; and finally the pendulum is temperature and barometrically compensated. I think Dave's distribution looks very gaussian (normal) and is actually a very useful measure though not of Q! It tells us I think that the systematic variations are pretty small and most of the fluctuations are random, though they could be due either to the oscillator or the measurement system. No point in denying it - I'm worried, and have been since John emailed a couple of his papers to me last week . Not quite convinced myself yet I'm wrong about Q but I trust John's judgement in this area. So I spent this afternoon bashing my brains in hope of understanding it! Doesn't prove anything but I produced these similar graphs, also comparing normal and resonant curves: First up is my pendulum's frequency distribution. Second is my pendulum's frequency distribution fitted to a normal distribution. The match is good suggesting my pendulum is producing normally distributed periods. Third is a resonant curve generated from this formula found under 'Universal Resonance Curve' in Wikipedia's Resonance article:
ω is the natural resonant frequency Damping the third curve with a decay factor of 0.1 produces a curve similar to the actual pendulum distribution Fourth graph is the resonance curve generated with a lighter decay factor. As expected it produces a much sharper curve. No wonder I'm confused! Dave
|
| duncan webster | 18/08/2023 18:20:58 |
| 5307 forum posts 83 photos | Stepping gingerly as I'm not at all sure what I'm talking about, Dave's third and 4th curves relate to a resonant system being driven at a range of frequencies above and below the resonance. A pendulum is driven at its resonant frequency, or at say 1/15th for a Synchronome, or not at all when doing a run down test. I can't help feeling that these are 2 different scenarios. My pendulum keeps noticeable swinging for quite a long time if I turn the power off, can't exactly remember, but tens of minutes, does a inductor/capacitor manage this? If I had a pendulum which was perfect in every way apart from a bit of damping and I let it run down, the frequency would very gradually increase as the amplitude decayed, but it wouldn't have a normal distribution. |
| SillyOldDuffer | 18/08/2023 18:57:25 |
| 10668 forum posts 2415 photos | Posted by duncan webster on 18/08/2023 18:20:58:
... My pendulum keeps noticeable swinging for quite a long time if I turn the power off, can't exactly remember, but tens of minutes, does a inductor/capacitor manage this? ... An LC circuit of the same Q and resonant frequency as a pendulum would take the same number of cycles to decay and hence the same time. The decay formula is : However LC circuits usually oscillate at much higher frequencies than pendula, so the number of cycles needed for an LC resonator to decay to the same level occur much faster, An oscillator of Q=10000 at 10MHz decays 10 million times faster than one of Q=10000 oscillating at 1 Hz. Dave |
| Michael Gilligan | 18/08/2023 20:02:56 |
23121 forum posts 1360 photos | Posted by SillyOldDuffer on 18/08/2023 17:44:37: . […] Damping the third curve with a decay factor of 0.1 produces a curve similar to the actual pendulum distribution Fourth graph is the resonance curve generated with a lighter decay factor. As expected it produces a much sharper curve. No wonder I'm confused! Dave
. With the greatest respect and empathy, Dave … I think even a damping factor of 0.01 [your fourth graph] would be appallingly high for a pendulum. MichaelG. . Edit: __ in the case for the prosecution, I present this [found after I posted] well-documented, and easily replicated, experiment: https://arxiv.org/pdf/2002.03796.pdf Edited By Michael Gilligan on 18/08/2023 20:32:22 |
| John Haine | 18/08/2023 20:25:59 |
| 5563 forum posts 322 photos | Posted by duncan webster on 18/08/2023 18:20:58:
..... If I had a pendulum which was perfect in every way apart from a bit of damping and I let it run down, the frequency would very gradually increase as the amplitude decayed, but it wouldn't have a normal distribution. The period would decrease very slightly, but the cycle-to-cycle random variation would be very small unless there was a lot of noise affecting it (for example support vibration). |
| Michael Gilligan | 18/08/2023 20:40:58 |
23121 forum posts 1360 photos | … For appallingly, please read rather MichaelG. |
| Martin Kyte | 18/08/2023 20:41:02 |
3445 forum posts 62 photos | Not sure about the use of the general resonance formula as applied to an intermittently driven oscillator. ? regards Martin |
| SillyOldDuffer | 18/08/2023 21:59:10 |
| 10668 forum posts 2415 photos | Posted by Michael Gilligan on 18/08/2023 20:02:56:
Posted by SillyOldDuffer on 18/08/2023 17:44:37: . […] Damping the third curve with a decay factor of 0.1 produces a curve similar to the actual pendulum distribution Fourth graph is the resonance curve generated with a lighter decay factor. As expected it produces a much sharper curve. No wonder I'm confused! Dave
. With the greatest respect and empathy, Dave … I think even a damping factor of 0.01 [your fourth graph] would be appallingly high for a pendulum. MichaelG. . ...Oh dear, a major breakdown of communications! No wonder - it's getting complicated, My Graphs 3 and 4 are examples illustrating how the shape of a universal resonance curve depends on the damping factor. They're a response to John's post in which he compares a normal distribution curve to a resonant curve and suggests the curves move away from each other. I'm pointing out by example that the shape of a resonance curve can be made to look like a normal distribution by tweaking the decay factor. I said I don't believe it proves anything! This part of the discussion relates to a serious criticism John is making of the way I calculate Q-factor using what I believe to be the valid bandwidth method. Serious because I'm an amateur poking around in the dark, whilst this is John's area of expertise and he can do the maths! At the moment I'm in the unhappy position of not understanding my own work or understanding why John thinks I've got it wrong. My efforts this afternoon have shown my pendulum's frequency distribution is close to a normal distribution and that I can synthesise a resonance curve to take much the same shape. I'm no nearer proving to my own satisfaction that the way I calculate Q is right or wrong. Sadly, when an expert tells an amateur he's messed up, the expert is usually right...
Dave |
| SillyOldDuffer | 18/08/2023 22:13:28 |
| 10668 forum posts 2415 photos | Posted by S K on 18/08/2023 01:15:27:
If I estimate your "half power bandwidth" to be 2 times your standard deviation (that's the number I have, anyway), then after rounding the numbers for simplicity, I get Q=1/(2*0.001)=500. How do you get over 20,000? What numbers do you have? Also, you expressed concern about how your cumulative time error had wandered. This is due in large part to the accumulation of many small random errors in a classic random walk. If those small errors are 250 times lower (i.e., S.D. = 4us vs. 1ms), then the cumulative deviations should, in an typical run, also be 250 times lower. So yes, you do want as low a standard deviation as you can get. ...
An interesting development this afternoon! I found a code error. The standard deviation of my data isn't about 1mS, it's 0.037 milliseconds, which by SK's method above gives my pendulum Q=13500. Sorry about that, my fault. Assuming the data and method I'm using is correct, which has been strongly challenged by John, the 3db bandwidth of my pendulum is about 0.044 milliseconds, period 0.937357s. Dave |
| Michael Gilligan | 18/08/2023 22:25:27 |
23121 forum posts 1360 photos | Posted by SillyOldDuffer on 18/08/2023 21:59:10: […] Oh dear, a major breakdown of communications! No wonder - it's getting complicated, […] . mea culpa … but I would still recommend the brief paper that I linked. MichaelG. |
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - Winter Storage Of Locomotives
04/10/2023 21:02:11 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!












 Register
Register Log-in
Log-in


