JoNo's Pendulum
| SillyOldDuffer | 03/09/2023 21:01:22 |
| 10668 forum posts 2415 photos | Posted by Joseph Noci 1 on 03/09/2023 19:41:07:
Posted by John Haine on 03/09/2023 18:00:05: ... Twice mine - Mine obviously is lacking - what is your advice?My first suspect is the stand, because it's an important part of the system:
Try bouncing a laser pointer off a mirror placed on top so that any movement of the stand at the suspension is amplified at the distant dot. Might be interesting as well to measure Q with the stand stood on a soft rug rather than tiled floor. Dave
|
| Michael Gilligan | 03/09/2023 21:19:43 |
23121 forum posts 1360 photos | Posted by SillyOldDuffer on 03/09/2023 21:01:22:
Posted by Joseph Noci 1 on 03/09/2023 19:41:07:
Posted by John Haine on 03/09/2023 18:00:05: ... Twice mine - Mine obviously is lacking - what is your advice?My first suspect is the stand, because it's an important part of the system:
. As will be clearly demonstrated by the example of two pendulums mounted on a substantial beam gradually synchronising. [ sorry, can’t remember whom to credit ] MichaelG. .
https://physicsworld.com/a/the-secret-of-the-synchronized-pendulums/ Edited By Michael Gilligan on 03/09/2023 21:21:44 |
| duncan webster | 03/09/2023 21:30:55 |
| 5307 forum posts 83 photos | Friend of mine bought a Pulsynetic, it wouldn't run at all when stood on his carpeted floor, buts works nicely when bolted to a brick wall |
| Joseph Noci 1 | 06/09/2023 09:29:49 |
| 1323 forum posts 1431 photos | The last Q run now shows Q to be near to 14000. Q has been slowly increasing over the last 36hours of running - My setup is reasonably stable and consistent and I tend to trust the Q determination. I suspect the increase is all related to the knife pivot. The knife sits in the curve of the bearing inner race and I believe it is not always in the bottom of the curve after any mechanical work on the pendulum. The pendulum rocking motion plus gravity slowly lets the knife ride down to the lowest part of the curve and when there, there is no lateral force on the pendulum, which induces a lateral swing ( 90deg to the main swing..) When the knife is at the bottom the Q is good. Comfortingly, I have found a modulation on the angle sensor voltage output which started with a 10sec period ( the peak to peak voltage of the 0.5hz sine swing varies by 3 or 4 mV at 10sec period) and the period increased to with the mV delta now almost being almost indiscernible as the knife beds in. This I believe reinforces the knife bedding concept.
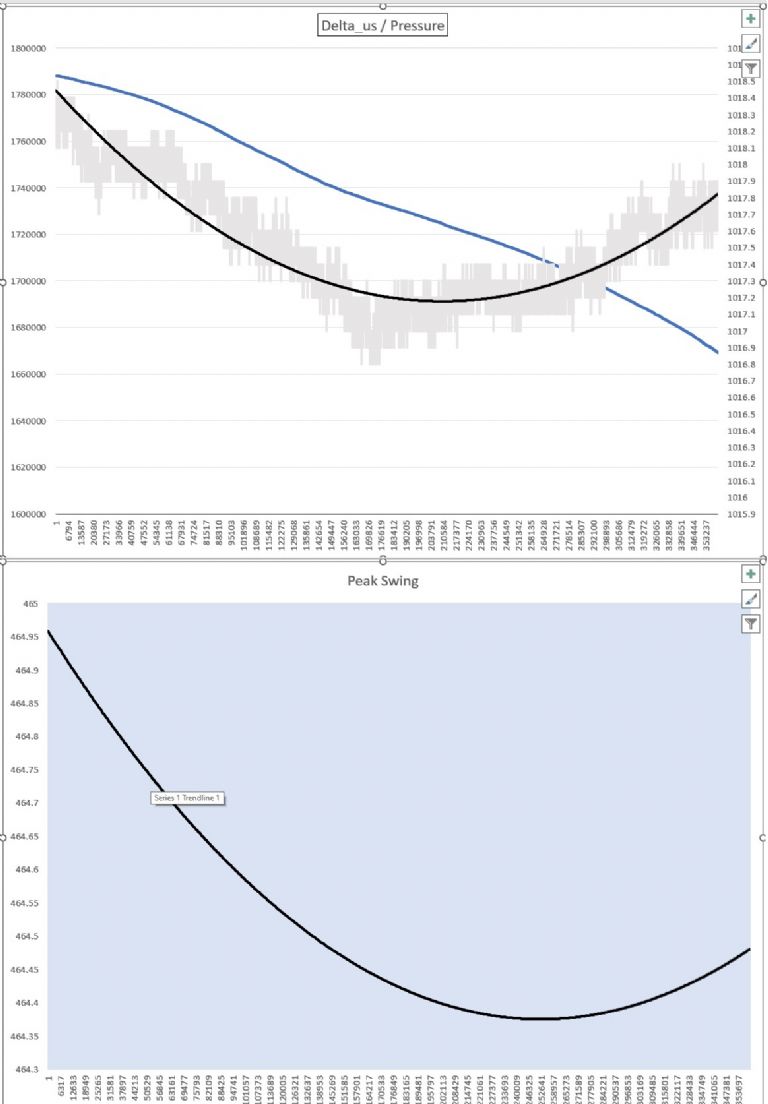
The pendulum period is presently measured against my GPSDO 0.5hz output. I sat and fiddled with the pendulum adjuster weights till the delta remained fixed , ie , no drift, at that moment and used that as my baseline. I logged lots of data over a large number of hours and the pendulum shows very well the period variation with ambient conditions. The ambient temp in the study does not change more than 2deg over 24hours and there seems little correlation between temp and period at this stage. The bob and the rod temp change by 1deg max over that period. Humidity is reasonably stable in the study - variation during logging was from 44% to 45.5%, and there seems to be no correlation between humidity and period change. Pressure, on the other hand, seems to dominate. The curves below: Top chart , left scale, Blue curve = delta in us, over 5 hours horizontal scale. ( 2,000,000 us - 2sec period) Top chart , right scale is pressure in millibar, max was 1018.4mb , min 1017.2mb Bottom chart - the peak swing in millivolts ( or millidegrees) of the pendulum - It follows the pressure curve nicely, with a phase shift that is close to the current control loop response time. This seems to show that the swing is increased as the pressure increases which 'sounds' correct - the bob is slowed as pressure rises so the swing reduces, and the system gain then increases to get the swing back up again. It makes sense, but I am not sure. This curve is the output of the peak detector that is fed by the sine swing from the angle sensor - Intuitively I would have thought that curve should be flat - If the sine peak reduces the gain increases, driving the coil harder, the swing increases back to the setpoint, and the swing level is back to setpoint. I am trying to extract the total control loop transfer function as that is key to the understanding I believe. A further complication, due to lack of suitable components - the Voltage variable gain amplifier I use is a linear-in-dB device - the angle sensor output is peak detected and finally drives the voltage control input of the VGA - a 33mv change is a 3dB gain change. So the control is logarithmic and the resulting bottom curve is also log, etc - I think there is great potential for the method of amplitude control, but there are too many unknowns for me and I am a bit lost! |
| Joseph Noci 1 | 30/09/2023 20:37:34 |
| 1323 forum posts 1431 photos | I have re-designed almost all the electronics on the pendulum. The new ideas implement better op-amp voltage offset and temp drift control and I have implemented a linear voltage controlled amplifier for the pendulum sinusoidal drive voltage amplitude control- this was logarithmic in the previous design and was very sensitive. Also, the 90deg drive signal phase shifter is now controlled via a 24bit DAC, from the Nucleo processor. The phase shifter gives plus and minus 5deg shift around 90deg with a -3v to +3v DAC control voltage. The amplitude control loop works well - it locks quickly and appears very stable I will post circuits etc later , for anyone interested. I am trying to determine the change in period wrt the change in phase at the moment, to see if I can derive a transfer function I can use in the final software control loop. This means setting the pendulum for a 'stable' drift rate and logging the period , and then changing the phase in 0.5deg steps while logging. From that I should be able to derive the change in period at phase change, and how that works through the system for some 10s of minutes after the change. This is interesting, since if the pendulum period is increased, for example, the amplitude had to have changed as well, and the amplitude control loop will try to bring that back into closed loop control. So, maybe the phase change will change the period, for a short while, till the amplitude loop stabilises again. Then removing the phase change repeats the process in the opposite direction - this is how it simulates anyway, so I think the phase change method of control will be an application of phase change for a short period, seconds, etc, just enough to affect the change in period, and then revert back to 90deg... Lots to learn down this road. I have a 'theory' question please... To mechanically adjust the pendulum period I have a nut under the bob that raises/lowers the bob, for coarse adjustment. At the top of the pendulum rod I have two adjuster nuts, one small (in yellow), another larger (in red), just below the pivot. These give very fine rate adjustment. As expected, if I lower the bob, the rate increases. However, if I screw the large adjuster nut DOWN (away from pivot, towards bob), the rate DECREASES, and UP INCREASES the rate. Can someone defend this mathematically?? Edited By Joseph Noci 1 on 30/09/2023 20:38:22 |
| Joseph Noci 1 | 30/09/2023 21:21:27 |
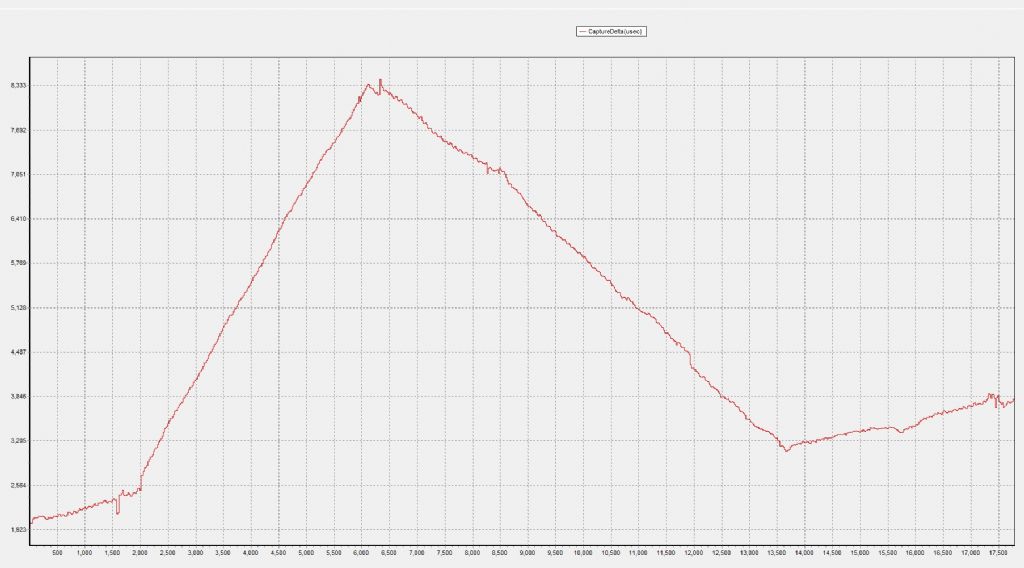
| 1323 forum posts 1431 photos | A quick plot of Phase angle change and effect: X axis is elapsed time in 100ms periods. Y axis is pendulum period delta from GPSDO 0.5Hz reference. The left rising slope: Commanded phase angle = 86deg. duration is 400seconds, with a pendulum period change of 5769us over said 400sec, giving a pendulum period increase of 0.005769sec in 400sec The right falling slope:: Commanded phase angle = 93deg. duration is 700seconds, with a pendulum period change of 5128us over said 700sec, giving a pendulum period decrease of 0.005128 sec in 700sec. I believe this may just work... |
| S K | 30/09/2023 22:46:03 |
| 288 forum posts 42 photos | First, I think you mean that the period increases when you lower the bob, not the rate. If you add mass right at the pivot, there will be no impact on the period at all. If you lower the adjustment nut, the period will decrease. Think of that mass as detracting from the mass of the bob. If you add mass below the bob, the period will finally increase. That's assuming that the rod is very light and the bob is very heavy, meaning that the center of mass and the radius of oscillation are both inside the bob. In the other extreme, imagine a pendulum consisting only of a heavy rod (no bob). For this, the radius of oscillation is 2/3 down from the pivot. Add weight above that, and the period will decrease. Add below that, and it will increase. Edited By S K on 30/09/2023 22:58:30 |
| Joseph Noci 1 | 01/10/2023 07:25:12 |
| 1323 forum posts 1431 photos | Posted by S K on 30/09/2023 22:46:03:
First, I think you mean that the period increases when you lower the bob, not the rate. If you add mass right at the pivot, there will be no impact on the period at all. If you lower the adjustment nut, the ............ Add weight above that, and the period will decrease. Add below that, and it will increase.
Apologies, thanks for correcting me - period is what I meant, and thanks for the explanation Joe |
| John Haine | 01/10/2023 08:31:53 |
| 5563 forum posts 322 photos | Standard expression for effect of phase error on fractional change in rate is Tan(phase error)/2Q Which is one reason why high Q is desirable. |
| SillyOldDuffer | 01/10/2023 11:55:45 |
| 10668 forum posts 2415 photos | Posted by Joseph Noci 1 on 06/09/2023 09:29:49: ...Pressure, on the other hand, seems to dominate. The curves below: ...seems to show that the swing is increased as the pressure increases which 'sounds' correct - the bob is slowed as pressure rises so the swing reduces, and the system gain then increases to get the swing back up again. It makes sense, but I am not sure. ...Would have commented at the time except I missed this interesting post. I'm fretting about barometric pressure because it's almost certain my approach to compensating for pressure change is wrong. Long story and I'm still working on it, but I was educated by this description found on physics.stackexchange:
By Archimedes' principle the effective weight of the bob is reduced by the buoyancy of the air it displaces, while the mass (inertia) remains the same, reducing the pendulum's acceleration during its swing and increasing the period. This depends on the air pressure and the density of the pendulum, but not its shape. The pendulum carries an amount of air with it as it swings, and the mass of this air increases the inertia of the pendulum, again reducing the acceleration and increasing the period. This depends on both its density and shape. Viscous air resistance slows the pendulum's velocity. This has a negligible effect on the period, but dissipates energy, reducing the amplitude. This reduces the pendulum's Q factor, requiring a stronger drive force from the clock's mechanism to keep it moving, which causes increased disturbance to the period. I'd assumed a simple linear relationship when it's complicated and non-linear! No wonder my clock doesn't work as intended. I haven't quite given up on compensating mathematically for changing air pressure, but running the pendulum in a vacuum is the easiest way of fixing the problem. My mind goes blank when I tackle the maths, and I'm already struggling with a paper John Haine sent me! Dave Dave |
| Joseph Noci 1 | 01/10/2023 14:02:22 |
| 1323 forum posts 1431 photos | Posted by John Haine on 01/10/2023 08:31:53:
Standard expression for effect of phase error on fractional change in rate is Tan(phase error)/2Q Which is one reason why high Q is desirable. John, what phase error do you mean? Or which phase(s) are used to define this error term? |
| duncan webster | 01/10/2023 16:17:51 |
| 5307 forum posts 83 photos | SK you're going to have to explain that, Joe isn't adding mass, he's moving an existing mass. I'd expect moving the little nut down and leaving everything else alone to effectively lengthen the pendulum and so increase period |
| John Haine | 01/10/2023 18:19:04 |
| 5563 forum posts 322 photos | Posted by Joseph Noci 1 on 01/10/2023 14:02:22:
Posted by John Haine on 01/10/2023 08:31:53:
Standard expression for effect of phase error on fractional change in rate is Tan(phase error)/2Q Which is one reason why high Q is desirable. John, what phase error do you mean? Or which phase(s) are used to define this error term? The phase difference between the impulses and BDC of the pendulum. In your case with a sinusoidal drive the maximum drive torque is ideally at BDC. |
| John Haine | 01/10/2023 18:22:21 |
| 5563 forum posts 322 photos | Posted by duncan webster on 01/10/2023 16:17:51:
SK you're going to have to explain that, Joe isn't adding mass, he's moving an existing mass. I'd expect moving the little nut down and leaving everything else alone to effectively lengthen the pendulum and so increase period Any majss added above the CG of the pendulum moves the CG up and effectively shortens it. For a given added mass its effect is maximum half way down the road, minimum at the bottom and top. |
| duncan webster | 01/10/2023 18:35:34 |
| 5307 forum posts 83 photos | But he isn't adding mass, he's moving existing mass down (unless I've completely misunderstood what Joe wrote However, if I screw the large adjuster nut DOWN (away from pivot, towards bob), so the cg goes down. Not like adding pennies to Big Ben. if m is the little mass and its distance is d, M is bob mass and its distance is D, distance of cg from hinge = (m*d +M*D)/(m+M) which increases as d increases |
| S K | 01/10/2023 19:12:16 |
| 288 forum posts 42 photos | Considering a simple pendulum (weightless rod, point-mass bob): Sure, if you are not adding mass but merely lowering an adjustment weight, the CG shifts down. But the CG isn't the main point, the radius of oscillation is. That's the position that the point-mass bob would be if you converted a compound pendulum (bob plus adjustment weight) to an ideal pendulum with the same period. Slide the adjustment weight all the way to the top, and that weight becomes irrelevant to the period since it's not even swinging. Slide it all the way down to the bob, and it's also irrelevant! Why? Because now you just have a heavier bob, and the period isn't dependent on the mass of the bob! (T=2*Pi*sqrt(L/g) - the mass m of the bob is not in the equation.) The CG is obviously quite different in those two cases, but the result is the same - no change in period! Slide it to somewhere near the middle, though, and now you have distinctly changed both the CG and the radius of oscillation. In that case, the compound pendulum is like an ideal pendulum with the bob higher up than before, hence a reduction in the period (the pendulum swings faster). This effect is at a maximum when the adjustment weight is at the middle of the rod. You have to put the adjustment weight below the bob to increase the period. It becomes a bit more complicated when the rod is heavy and the bob is light in comparison. Then, the radius of oscillation is already above the bob, so lowering an adjustment weight below that point (but still above the bob) can increase the period. That result came up in my very light "gravity pendulum," but wouldn't often be the case for a more typical pendulum (carbon fiber rod, very massive bob that's extended in space) that folks are making here. Edited By S K on 01/10/2023 19:29:01 |
| duncan webster | 01/10/2023 21:52:41 |
| 5307 forum posts 83 photos | well blow me down! I was so troubled by this that I had to do some sums. I took a pendulum with a bob 10 units in mass suspended 10 units from a hinge and then slid a 1 unit mass down the rod in 1 unit increments. Lo and behold the Equivalent Length starts at 10, goes down to 9.76 at 5 units, then back up to 10. the distance to the cg starts at 9.09 and goes up steadily to 10
If anyone wants to repeat the exercise, according to wikipedia the Equivalent Length is (m*d^2+M*D^2)/(m*d+M*D), using the same nomenclature as before. You're never too old to learn something! If it wasn't such a pain to import an image I'd paste it in Edited By duncan webster on 01/10/2023 21:55:16 |
| Joseph Noci 1 | 03/10/2023 08:42:32 |
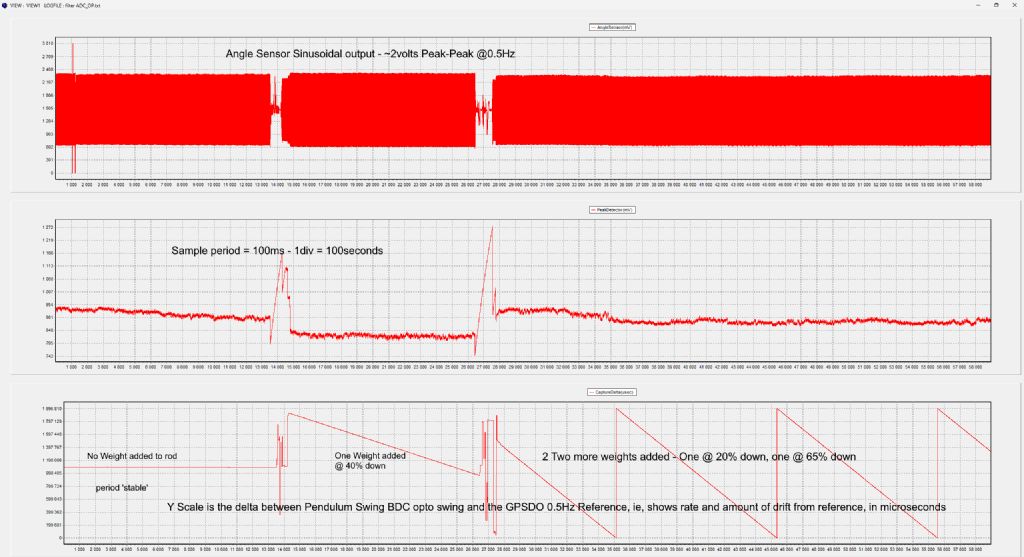
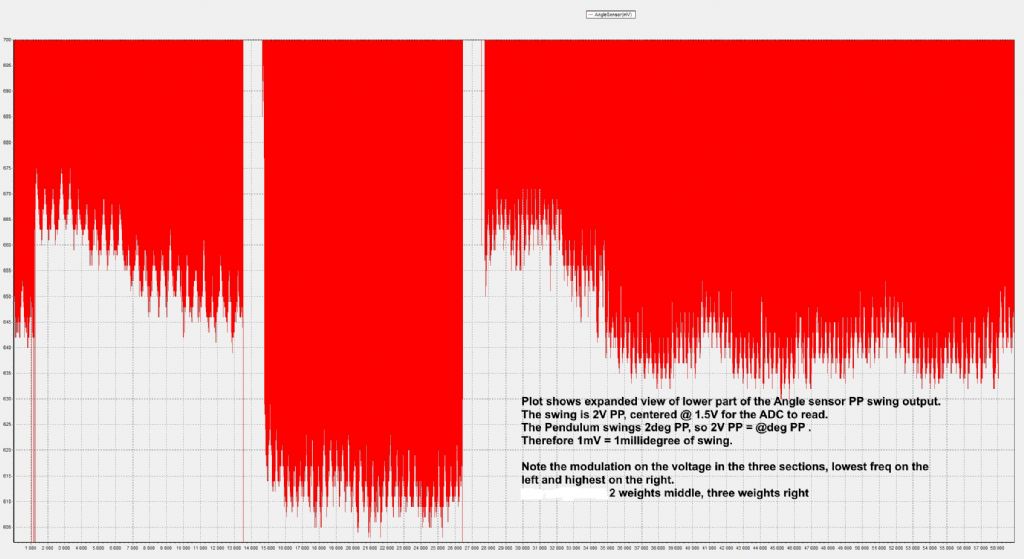
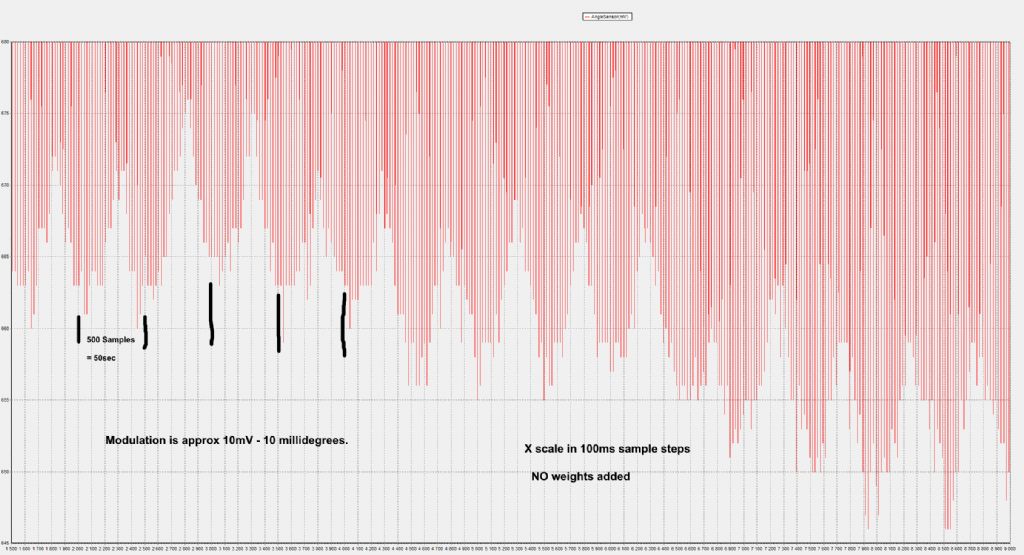
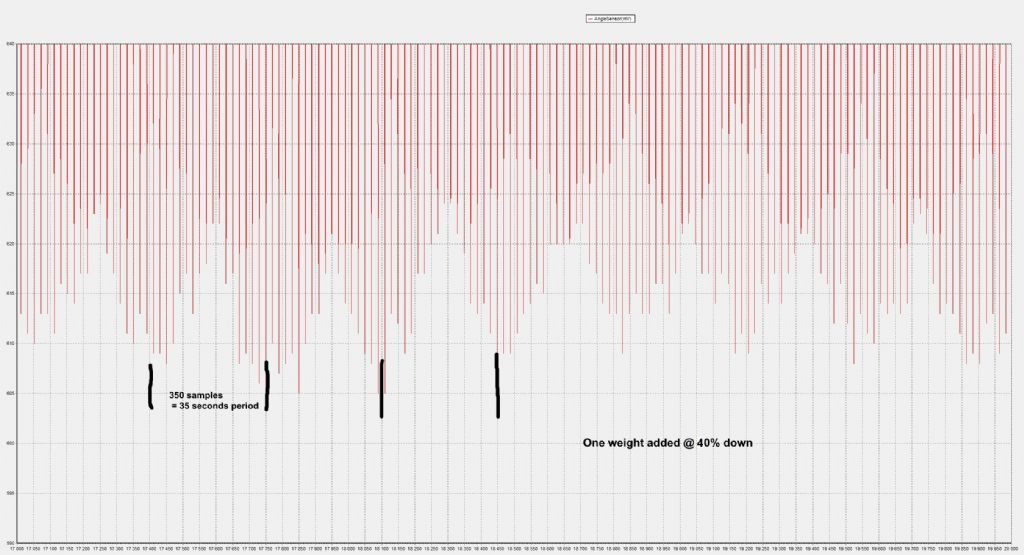
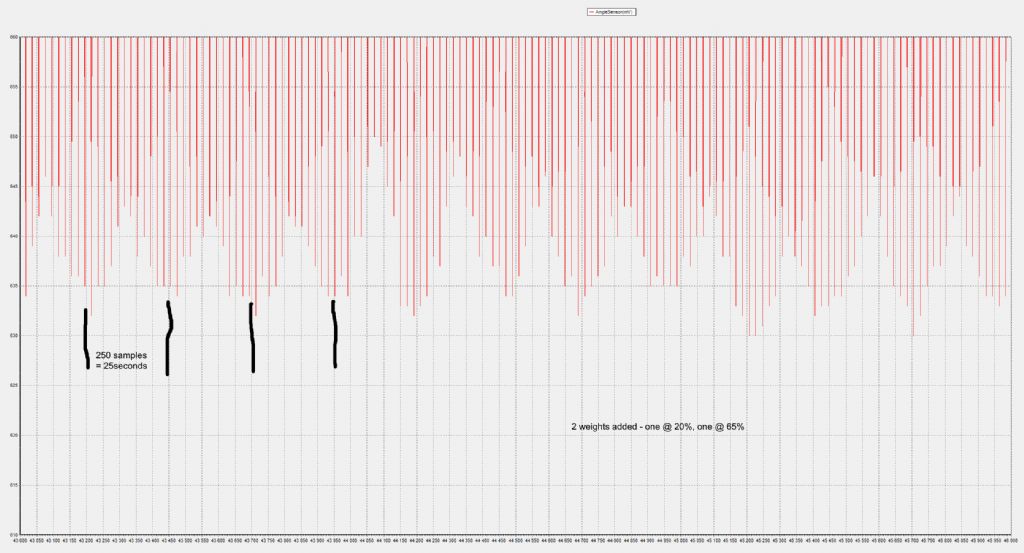
| 1323 forum posts 1431 photos | My pendulum exhibits an interesting rod 'vibration' mode.. I suspect this is inherent in all pendulums but passes unobserved due to the way the period is measured by most folk. Since my pendulum is amplitude controlled by measuring the PP swing sinus voltage, the quality of that measurement is key to generating a clean stimulation sinusoid. The PP measurement is done by means of a 2 op-amp Peak detector ( typical 3 diode/op amp peak detector). My PP swing logging shows noise, which I believe stems from the peak detector - the peak detector works by 'topping' up a storage capacitor to the peak value of the sinus, but the opamp that generates this top-up voltage operates open-loop til top-up time, and the top-up interval seems to vary, which means the peak voltage on the storage cap varies, which means my drive voltage to the pendulum coil varies... Not much, 8 to 14mv, which equates to 14 millidegrees swing variation max. I am still unsure how to equate 14 millidegrees variation to a ppm value in pendulum stability... However.. In pursuing a cleaner PP measurement method, I notice a regular modulation on the logged PP swing sinus - at first I thought this was the Peak detector somehow feeding through - I replaced the peak detector output with an equivalent fixed voltage. The pendulum was now not amplitude controlled, but was driven, with no peak detector artifacts able to affect it. Made no change. I then disconnected the sinus drive to the pendulum coil, and let is run down to 10% swing. Made no difference to the modulation phenomena - did a Q calc to verify the pendulum is still 'OK' - Q = 12900, so OK. Then I reconnected every thing up, did a run and logged it - This shows a modulation depth of around 10mv - 10milligrees at a 50 second period. I then moved/fiddled with the knife pivot location point, ie, moved the knife forward about 0.2mm, so it was 'riding' up the inner ball race support surface. This meant the knife was twisted in its circular support pivot, and would add some odd motion to the swing. I then logged data again - I did observe a new modulation on the Swing sinus, but at a 2sec period, ie, same as the pendulum period - I could also see the bob was swinging in an ellipse, rather than a straight line. However, the 50sec modulation period remained unchanged, so it was not induced by the knife or pivot or its friction, etc. I then added a weight to the pendulum rod - an AA penlight cell fitted with masking tape.. - at 40% down from pivot, and logged data - This showed the same modulation depth approx, but the period was now 35 seconds. I then added 2 more weights ( AA cells) one at 20% down, one at 65% down. The period changed to 25 seconds. So - the rod somehow has a very long period vibration mode, or a High frequency vibration mode, which influences the pendulum period in a very cyclic manner. I suspect everyone using light weight 'stiff' rods has similar modes, but do not see them due the to measurement methods. This shows the three logs, no weight, one weight 3 weights. Expanded view of the bottom peaks of the sinus swing, shows the 3 varying modulation frequencies No weight 1 Weight
The carbon fibre tube is a no-no - maybe a solid carbon fibre rod will improve matters, but that prevents fitting wires internally to my sensors in the rod and bob. And solid carbon rods temp coef is a lot poorer than a tube, so I would be better off using Invar... And I am pretty sure the house is not vibrating at those frequencies... The issue is evaluating how much of an effect this modulation has on the pendulum period - it is cyclic, 10 millidegrees, which can be validated in change of period, but the cyclic nature undoes what it causes on a regular basis. Not sure if I am chasing ghosts here.
Edited By Joseph Noci 1 on 03/10/2023 08:49:25 |
| Joseph Noci 1 | 03/10/2023 10:47:09 |
| 1323 forum posts 1431 photos | I have been digging in internet to try find some info on this phenomena and come up dry. Searching 'pendulum rod' vibration brings up people who call the pendulum swing a vibration, and the rod vibrates at pendulum period...Even Alan Cromer's 'many oscillations of a rigid rod' does not help... What is also interesting is that the modulation frequency as described has seemingly no relationship to the rod's 'Twang' ( there's that word again) frequency, which is in the many 10s of Hz region. Edited By Joseph Noci 1 on 03/10/2023 10:47:20 |
| Michael Gilligan | 03/10/2023 12:13:12 |
23121 forum posts 1360 photos | Posted by Joseph Noci 1 on 03/10/2023 08:42:32:
My pendulum exhibits an interesting rod 'vibration' mode..
[…]
So - the rod somehow has a very long period vibration mode, or a High frequency vibration mode, which influences the pendulum period in a very cyclic manner. […]
. That is VERY interesting Jo, but I honestly can’t imagine any single vibration mode of your pendulum which could have that [those] period[s] … I therefore suspect that you are seeing a ‘beat frequency’ between two other modes. How the devil to identify them is way beyond my ability. MichaelG. |
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - Winter Storage Of Locomotives
04/10/2023 21:02:11 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!












 Register
Register Log-in
Log-in


