Pendulum 'Q' value and measurement methods
| Michael Gilligan | 11/08/2023 16:27:53 |
23121 forum posts 1360 photos | < phew > |
| SillyOldDuffer | 11/08/2023 16:37:34 |
| 10668 forum posts 2415 photos | Posted by John Haine on 11/08/2023 10:26:34:
Posted by SillyOldDuffer on 08/08/2023 20:25:21:
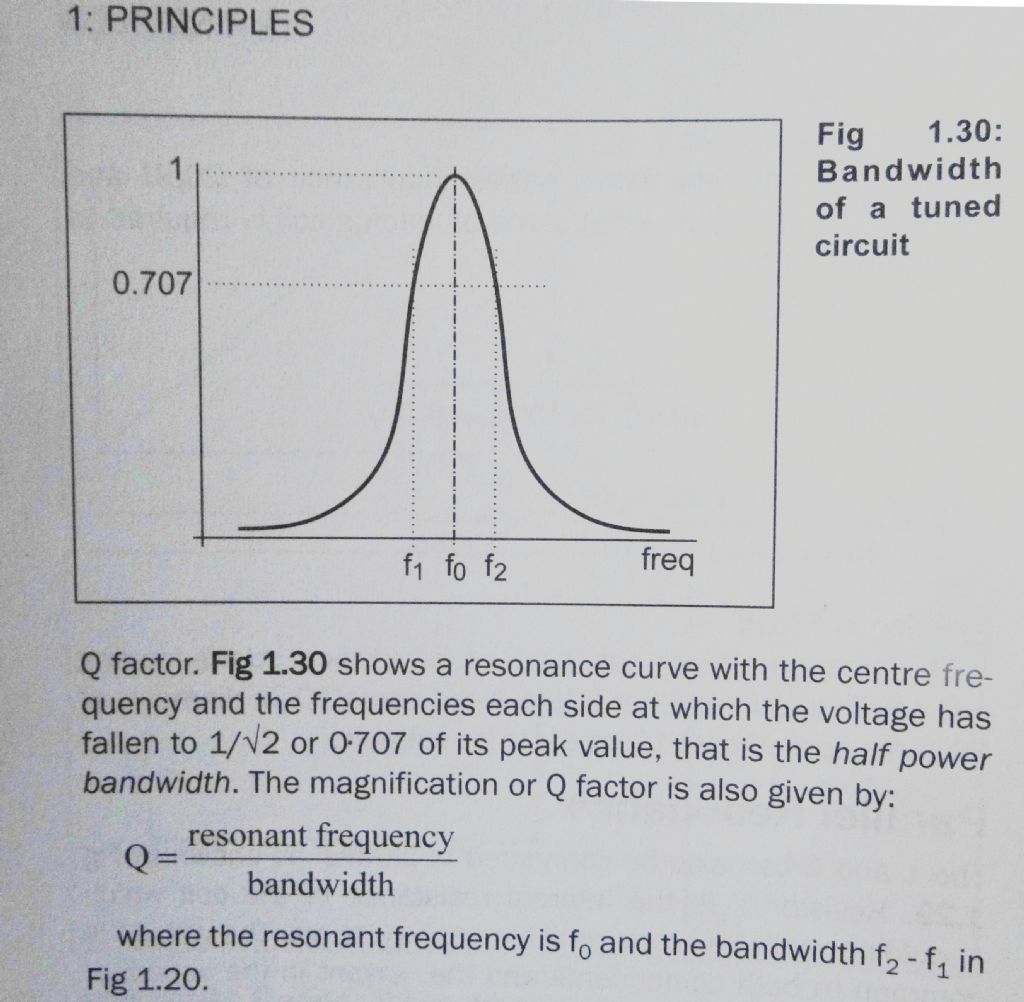
... Bandwidth is calculated from the 29.3, 50,0 and 70.7 percentiles. .... Dave Why do you choose those Dave? The bandwidth would normally be calculated from the "3dB down" points but it isn't obvious to me how "3dB down" = 0.7071 maps on to a percentile of a period distribution. ... All my clock books have disappeared! Luckily the gremlins forgot to hide my Radio library, and the same idea is in Dennison, Lorek (editors), 2005, Radio Communication Handbook 8th Edition, Radio Society of Great Britain Snip from page 1.16: And also discussed on this website. Might seem surprising that a pendulum and tuned circuits follow the same Physical Laws, but both involve oscillations. I have more background in communications than clocks, so tend to think of pendula as oscillators, emitting signals with a bandwidth, allowing me to use the maths and electronic techniques I'm familiar with to model them. Dave
Dave |
| SillyOldDuffer | 12/08/2023 11:28:07 |
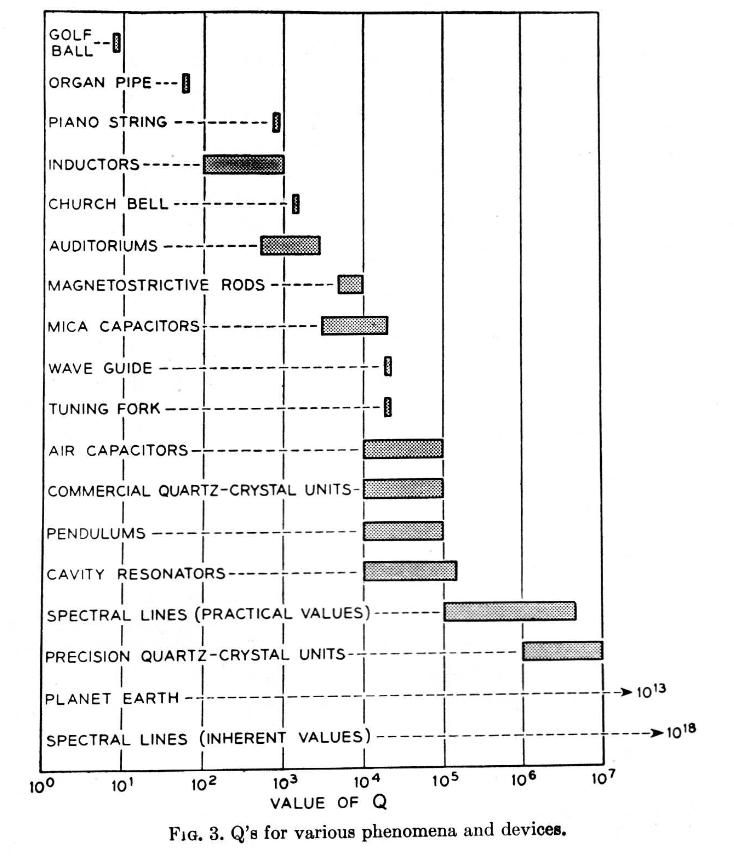
| 10668 forum posts 2415 photos | I also came across Estill I Green, (1955) "The Story of Q", a not too mathematical history of Q and its wider adoption. This comparative table is useful: and it mentions the relationship between Q and Power Factor, which I hadn't twigged must exist. Dave |
| Michael Gilligan | 12/08/2023 12:46:32 |
23121 forum posts 1360 photos | An excellent find, Dave … I will read it properly after some essential gardening Weather is suitably mild at last !
MichaelG. |
| Michael Gilligan | 12/08/2023 21:01:30 |
23121 forum posts 1360 photos | For the sake of completeness [and probably nothing more], here is Johnson’s patent: **LINK** https://worldwide.espacenet.com/patent/search?q=pn%3DUS1628983A MichaelG. |
| S K | 16/08/2023 14:26:24 |
| 288 forum posts 42 photos | Dave: Something continues to bother me about your method and your obtained value of Q. I am not doubting the fundamentals of the method (much), but the numbers do not seem to make sense in relative terms. You appear to be getting about 1ms standard deviation in your period measurements, whereas in my last test I'm getting about 4us; a factor of 250 difference. Not all is equal, but assuming that the bandwidth is strongly tied to those numbers (i.e., 250 times lower S.D. means 250 times narrower bandwidth), then using your method I should get a Q that is very approximately 250 times yours. That would not remotely make sense. What am I getting wrong or not seeing? Edited By S K on 16/08/2023 14:37:23 |
| S K | 16/08/2023 16:26:09 |
| 288 forum posts 42 photos | Well, I used Dave's method on my pendulum data, as far as I understand it (and I may not), and got a "Q" of 190,000. That's not possible. |
| John Haine | 16/08/2023 17:32:38 |
| 5563 forum posts 322 photos | If I may I'd like to comment on Dave's method. It seems to me that the resemblance of the normal distribution curve to a resonance curve is tempting but unfortunate. Assuming that Dave's period distribution is normal, its width is characterised by just one parameter, the standard deviation. The "-3dB" points are related to this but superfluous. In practice the width of the period distribution must depend on the amplitude and noise level (i.e. the "signal to noise ratio" as well as on Q. So buried in Dave's computation is this SNR, which itself is also determined by Q (as this determines the bandwidth of the noise which is affecting the period). So one can't take the width of the distribution compared to the mean as the Q since actually if the noise was zero Q would apparently be infinite! Some time back I looked at this and I think this equation for the rms period variation is accurate for a pendulum with small swing, in equilibrium amplitude, at frequency Fo, Q, amplitude a, and mass m, where N is the spectral density of the noise force component of the impulse. To compute Q from this you would need to know N. Pendulum Q can be measured most directly by a run-down test. Electronics Q is generally best measured as bandwidth or sometimes magnification factor. |
| SillyOldDuffer | 16/08/2023 21:15:50 |
| 10668 forum posts 2415 photos | After reading SK and John's posts I decided to pour myself a couple of large sherries and go to bed early!
Dave |
| John Haine | 16/08/2023 22:29:49 |
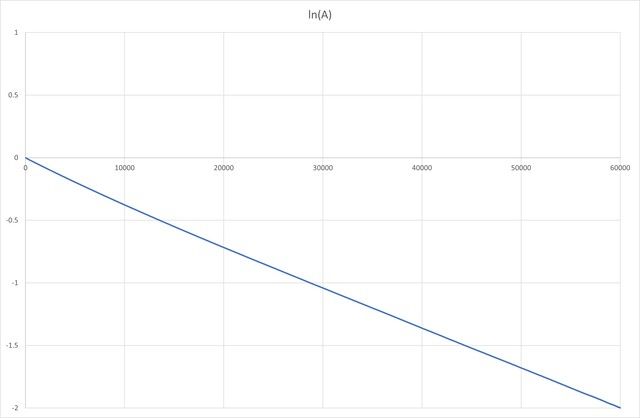
| 5563 forum posts 322 photos | I thought that the following example of a run-down test might be useful. I took this from my new pendulum just after replacing the spring and rod. Essentially allowed the amplitude to stabilise at just above the intended operating point, then switched off the impulsing and logged amplitude as it decayed, measuring it basically by the photogate time. The plot shows the natural log of amplitude against beat time (essentially seconds). Nearly a straight line with a barely visible "kink" after about 15000 seconds. The first part of the run (around the eventual operating point) yields a Q of about 22,500. Andrew Millington pointed out that the Q improves at lower amplitude to about 24,500. There are essentially two flow regimes around the bob it would seem, at larger amplitudes there is an increasing square-law dependence of drag on velocity whereas at lower amplitude it is essentially linear. Note that the curve is very clean with very little scatter of the points about the trend line.
|
| duncan webster | 16/08/2023 23:24:28 |
| 5307 forum posts 83 photos | So if SOD measured Q by rundown and got the same answer as by bandwidth the argument would be resolved. I must admit some doubt over trying to measure energy loss whilst putting energy in feels problematical. Of course he might already have done this and reported it previously, my attention span isn't what it was. |
| Joseph Noci 1 | 17/08/2023 07:20:44 |
| 1323 forum posts 1431 photos | Posted by John Haine on 16/08/2023 22:29:49:
I thought that the following example of a run-down test might be useful. I took this from my new pendulum just after replacing the spring and rod. Essentially allowed the amplitude to stabilise at just above the intended operating point, then switched off the impulsing and logged amplitude as it decayed, measuring it basically by the photogate time. The plot shows the natural log of amplitude against beat time (essentially seconds). Nearly a straight line with a barely visible "kink" after about 15000 seconds. The first part of the run (around the eventual operating point) yields a Q of about 22,500. Andrew Millington pointed out that the Q improves at lower amplitude to about 24,500. There are essentially two flow regimes around the bob it would seem, at larger amplitudes there is an increasing square-law dependence of drag on velocity whereas at lower amplitude it is essentially linear. Note that the curve is very clean with very little scatter of the points about the trend line.
That looks nice John. Would you refresh me please - what is your pendulum structure? - pivot style, bob ( shape, weight) rod material, and measurement method ( opto interrupter / part number)? There are now so many topics running on pendulum, I did not manage to find your earlier descriptions and references! |
| John Haine | 17/08/2023 07:29:04 |
| 5563 forum posts 322 photos |
All the information in that thread Joe. |
| John Haine | 17/08/2023 09:47:26 |
| 5563 forum posts 322 photos | Wikipedia has a good collection of information on Q. Includes a couple of useful formulae. Time constant of decay T = 2Q/Wo where Wo = 2pi/To (To is the full period). Then amplitude decays at A = Ao.exp(-t/To). Setting A/Ao to various convenient values such as 0.5 or 1/e then gives the various formulas for Q in terms of number of cycles that have been quoted. |
| Joseph Noci 1 | 17/08/2023 10:40:00 |
| 1323 forum posts 1431 photos | Posted by John Haine on 17/08/2023 07:29:04:
All the information in that thread Joe. Thanks John - refreshed ... |
| SillyOldDuffer | 17/08/2023 11:52:45 |
| 10668 forum posts 2415 photos | Posted by SillyOldDuffer on 16/08/2023 21:15:50:
After reading SK and John's posts I decided to pour myself a couple of large sherries and go to bed early!
Dave Last night's exciting episode ended with our hero (me because I'm writing the script) assailed on all sides. By analogy I was cuffed inside a heavily weighted crate dropped into the Atlantic north of Scapa Flow. Fortunately I'm a pulp fiction fan, where cliffhangers are resolved in the next issue with the line 'With one mighty bound he was free." Oh well, back to the real world where I may be sunk without trace! SK repeated my description of the bandwidth Q-factor calculation on his data and got an absurd answer. I don't think that proves the bandwidth method doesn't work. I'd like to run SK's data through my program to see what I get. If I get 198,000 too, then the clearly my approach is wrong. Any chance of making the data available via Dropbox or similar? John Haine is more difficult to deal with because I'm well out of my depth with the maths! John said (full post above at 17:32 yesterday): It seems to me that the resemblance of the normal distribution curve to a resonance curve is tempting but unfortunate. Assuming that Dave's period distribution is normal, its width is characterised by just one parameter, the standard deviation. The "-3dB" points are related to this but superfluous. In practice the width of the period distribution must depend on the amplitude and noise level (i.e. the "signal to noise ratio" as well as on Q. So buried in Dave's computation is this SNR, which itself is also determined by Q (as this determines the bandwidth of the noise which is affecting the period). In response, I didn't invent the Bandwidth method of determining Q-factor! As I understand it Q-factor is a dimensionless indicator of the goodness of an oscillator. Any oscillator from bouncing balls to atomic clocks. To my mind a pendulum is just another oscillator following the same rules as all the others. Oscillators resonate at a particular frequency, and energy is required to keep them going. Lossy oscillators, such as a pendulum in treacle, have low Q because stirring treacle consumes lots of energy. The same pendulum swinging in a vacuum has high Q because atmospheric friction is eliminated. Exactly the same rules apply to Inductor(L) / Capacitor (C) oscillators. Although capacitors are low-loss, the inductor is a metallic wire coil and the wire is a resistor. The same inductor made of Brass wire has lower Q than one made of Copper, and Silver is better again. Energy loss in a resistive inductor behaves the same way as energy loss in a pendulum overcoming air resistance. Two ways of measuring oscillator Q:
John said: 'seems to me that the resemblance of the normal distribution curve to a resonance curve is tempting but unfortunate. I disagree - I think the resonant curve of an oscillator is normally distributed unless something disturbs it. Standard Deviation isn't the whole story because, as far as I know, it doesn't describe the shape of the distribution, narrow or wide. Stdev has a dimension, whereas Q is dimensionless. I can't argue with John's formula, but offer this from an article on the web: This formula doesn't introduce the spectral density of the noise force component of the impulse. Duncan suggests measuring my pendulum with both decay and bandwidth methods. Did that in the past and got a result within about 30%. Not conclusive because I didn't repeat the measurement several times. Can't do a decay measurement on my clock at the moment because it's doing a long run. For family reasons I'm short of time at present, but might find a few hours to hack a test pendulum. Alternatively, if John has decay measured one of his pendula, and has a run log, I could analyse that to see if results are similar. Though chest deep in doubt, I still think Decay and Bandwidth are both valid ways of measuring pendulum Q. Dave
|
| John Haine | 17/08/2023 16:08:50 |
| 5563 forum posts 322 photos | Though chest deep in doubt, I still think Decay and Bandwidth are both valid ways of measuring pendulum Q. Absolutely they are - but I don't think your probability distribution of period is a bandwidth measure. |
| SillyOldDuffer | 17/08/2023 17:49:54 |
| 10668 forum posts 2415 photos | Posted by John Haine on 17/08/2023 16:08:50:
Though chest deep in doubt, I still think Decay and Bandwidth are both valid ways of measuring pendulum Q. Absolutely they are - but I don't think your probability distribution of period is a bandwidth measure. OK, but what am I measuring then? In my set-up a crystal oscillator measures the period of each beat of a pendulum, outputting a long list of similar values, standard deviation about 1mS. Averaging the list gives a value, 0.933558s, which is close to the period predicted by the usual formula from my pendulum's length. Further, plotting the distribution of periods from the list gives the bell curve expected of an oscillator. If the peak of my bell curve gives the pendulum's correct frequency, why don't the 3dB points on the same curve give Q? As period and frequency are equivalent, I think my data represents a spectral distribution. I'm not understanding why it's different from a resonant curve. Gosh my head hurts!
Dave
|
| S K | 17/08/2023 18:13:38 |
| 288 forum posts 42 photos | Are you really using the simplistic formula from that "bandwidth of a tuned circuit" diagram? That delivers a Q of about 500, doesn't it? What formula are you actually using? The thing is, with an S.D. of 1ms, I don't see how you can find all that much more than that with any similar bandwidth based formula. You need to focus on improving the S.D. first. If I had to guess, your measurement apparatus is probably to blame, not your pendulum. Edited By S K on 17/08/2023 18:18:45 |
| SillyOldDuffer | 17/08/2023 19:21:46 |
| 10668 forum posts 2415 photos | Posted by S K on 17/08/2023 18:13:38:
Are you really using the simplistic formula from that "bandwidth of a tuned circuit" diagram? That delivers a Q of about 500, doesn't it? What formula are you actually using? The thing is, with an S.D. of 1ms, I don't see how you can find all that much more than that with any similar bandwidth based formula. You need to focus on improving the S.D. first. If I had to guess, your measurement apparatus is probably to blame, not your pendulum. ... I am using the 'simplistic formula' for bandwidth. As far as I know it is valid - it's in all my books! Do you have an alternative? The diagram is from a Radio Communications Handbook, where Q= 500 is about right for an ordinary inductor/capacitor resonator at radio frequency. It doesn't represent the Q of a pendulum, quartz crystal or anything and else, just the typical shape of a resonance bell-curve. It's how narrow the curve is at the 3dB down points that decides Q. In the example below, all three curves are of the same form but Q=1 results in a low hump, whilst Q=100 gives a sharp peak:
As I said to John in a related thread, the Q calculation I'm using reports period consistent with the physical length of my pendulum. If the calculation gets period right at the 50 percentile, why should it be wrong at 70.7 and 29.3 percentiles? In an earlier post you said applying the bandwidth method to your pendulum gave Q=190,000. Can you share the data and calculation please, showing working. Might highlight what I'm doing wrong! Though related there's a difference between Q and standard deviation. In my simple view Q is a measure of how much energy is needed to drive a pendulum, whilst standard deviation is a measure of the pendulums frequency stability. I'm not too worried about by pendulum's high standard deviation because I've not found any evidence, yet, that it's related to the rate wandering. At the moment the clock is 14 seconds out in 2,835,926 which is 4.9 parts per million, so not disasterous. What's worrying me is the rate isn't altering at a steady rate, or changing with temperature or pressure. I'm letting it gather more data in hope a pattern emerges. Dave
|
Please login to post a reply.
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- hemingway ball turner
04/07/2025 14:40:26 - *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!

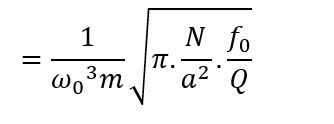
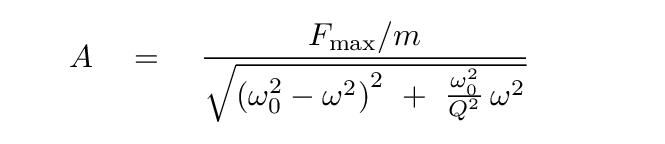










 Register
Register Log-in
Log-in


