Member postings for John Haine
Here is a list of all the postings John Haine has made in our forums. Click on a thread name to jump to the thread.
| Thread: Isochronous knife edge suspension? |
| 03/09/2023 21:05:35 |
But they aren't, as Philip's diagram shows. |
| Thread: JoNo's Pendulum |
| 03/09/2023 18:00:05 |
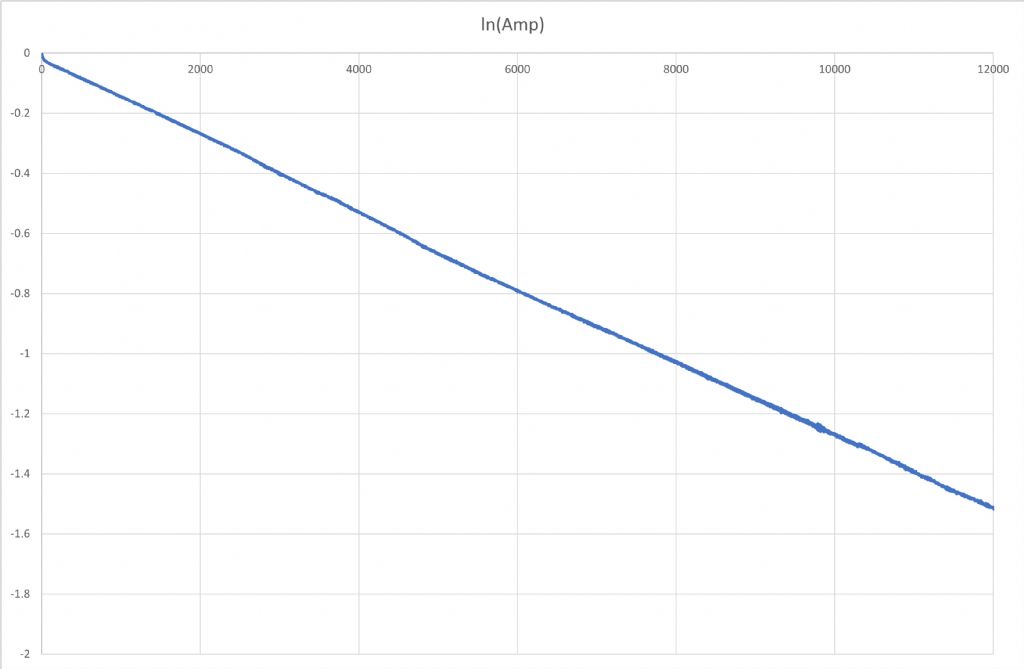
I just thought I should repeat the rundown test on my own new pendulum so it has been coasting down since 1pm. Again the log of normalised amplitude is -1 at 14612s in, so the same formula gives a Q of ~23,000, roughly what I got before. Edited By John Haine on 03/09/2023 18:01:45 Edited By John Haine on 03/09/2023 18:23:13 |
| 03/09/2023 17:42:45 |
"The fact that there is a DC offset there should no really affect the Log though?" Very much so I'm afraid. An offset in an exponential, like exp(x+k) just results in a scaling: exp(x+k) = exp(k) x exp(x) Logs are different: But log(x+k) = log(x) + log(1+k/x) (according to Wikipedia). |
| 03/09/2023 16:42:13 |
One thing to add is that this seems to show that the loss mechanism is nearly entirely simple viscous loss. |
| 03/09/2023 15:42:05 |
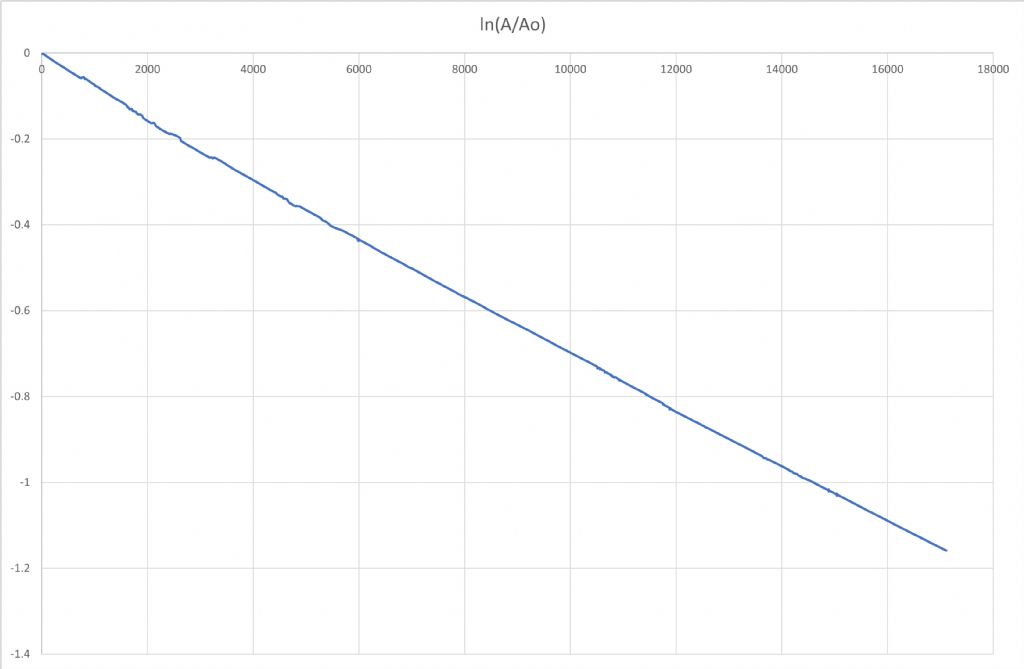
I've also had a go at the data that Joe was kind enough to share. He provided a file of essentially voltage samples from his angle sensor. These have a pronounced DC offset on them, larger than the negative peak, so I subtracted the mean value of all the readings from each to get a symmetrical waveform. There was also quite a lot of noise which made it hard to reliably find the peak so I did some crude filtering by replacing each value with the average of five (the sample plus the 2 before and the 2 after); then took the absolute value to include the negative peaks. Then extracted the peak readings using the Excel filter function. Normalised each sample to the value of the first and took the natural log to get this (for the first 12,000) seconds). That looks a pretty straight line to me! It reaches a value of -1 at 7800 seconds in, so the time constant is 7800 seconds. This is equal to 2Q/w where w is the angular resonant frequency, in this case 2pi x 0.5 = pi. Then Q = pi x 7800/2 = 12,250, very much in the ballpark Joes was measuring. I think the reason Joe was getting a strange decay shape was that he took the log of the peaks of the raw data which included the dc offset. Really awkward using Excel for this because there's so much data! Would be better to use something like R-Studio but I'm not sure it has all the functions needed.
Edited By John Haine on 03/09/2023 15:43:58 |
| Thread: Isochronous knife edge suspension? |
| 03/09/2023 12:30:33 |
Posted by david bennett 8 on 03/09/2023 05:10:27:
Please, can someone explain this paradox to me? ... If any one point on the rod follows a cycloid , why aren't they all? ... dave8 Edited By david bennett 8 on 03/09/2023 05:26:25 Edited By david bennett 8 on 03/09/2023 05:37:12 Though the point where the rod is attached to the roller may describe a cycloid, it's the wrong size for the bob which is much further away. And the CG of the bob (supposing all the system mass is concentrated there) actually describes a prolate trochoid not a cycloid as Woodward shows. So the system cannot be isochronous. I'm not sure what more one can say. Huygen's science does not assume a fixed suspension point, the bob is "suspended" from wherever the suspension cord instantaneously touched the cycloidal cheek. |
| Thread: JoNo's Pendulum |
| 01/09/2023 22:15:05 |
The natural log will just have the same numbers multiplied by a constant, which from memory is I think 2.302 [ln(10)] (could be wrong). Joe, could you email me the numbers behind one of the plots please? I could try to illustrate what I mean. |
| Thread: Isochronous knife edge suspension? |
| 01/09/2023 13:20:20 |
Think of a weight sliding down a symmetrical valley and up the other side with no friction. It will carry on going down and up again, oscillating to and fro with the same amplitude. What shape does the valley have to have such that the time taken for a single back and forth oscillation is the same irrespective of the amplitude? This shape is the "tautochrone" which is actually the evolute of a cycloid. But the evolute of a cycloid is itself the same cycloid but just shifted. For a pendulum, the weight is the bob, and so it has to move in a cycloid. The effective pendulum length is the radius (sorry, not diameter) of the generating circle. So if the weight is suspended by a rod the suspension has to arrange that the CoG of the bob moves in a cycloid with a generating circle of the same radius as the (maximum) rod length, for example using curved cheeks. Or arrange that it does so at least over a range of amplitudes of interest. Woodward showed that a roller on top of a plane support can't achieve this, but it's an open question whether a roller underneath a plane would work. For a roller arranged to roll on a plane, though a point on its circumference will roll in a cycloid, the generating circle has the same radius as the roller which is much smaller than the rod length. So the CG of the bob will not move in a cycloid (in fact it follows a trochoid) and the pendulum will not be isochronous (and nor in fact will the point on the roller where the rod is attached be). If you could arrange a weightless roller with the bob attached to its circumference, then it would be isochronous. There's an interesting mechanism that might be exploited that avoids magnets, called the Rolamite. I have seen an article discussing its application in a clock though not read in detail. |
| 01/09/2023 12:32:07 |
No, that doesn't follow. It's the CoG of the bob that has to follow a specific cycloid, with a generating circle diameter equal to the rod length. The generating circle for your configuration is the roller diameter. (This assumes that the mass is concentrated at the bob.) |
| 01/09/2023 11:50:01 |
Well I don't think isochronism is a concept applicable to a point! It's a property of the system as a whole. To put it another way, what do you mean by a point being isochronous? |
| Thread: Forum Platform Changes - PLEASE READ |
| 01/09/2023 09:12:10 |
Posted by JasonB on 01/09/2023 07:26:57:
Just a reminder to please make sure you know
... Jason, just to be clear, will the url remain the same please? For those of us that use password managers, then if it does this will remember the credentials for us. |
| Thread: JoNo's Pendulum |
| 01/09/2023 07:15:30 |
Posted by Joseph Noci 1 on 31/08/2023 08:10:22:
Posted by John Haine on 31/08/2023 07:14:37:
... After many hours of running and adjusting the weights I have it reasonably stable @ 0.5Hz with a 100us or so jitter. However, simply opening a 800mmx300mm cupboard door, 3 meters from the pendulum, causes a 3-400us jump within 1/2 a second of opening the door. The pendulum is in the study ( 2nd storey of the house..), on a thick concrete floor, but walking slowly on the floor 1 meter from the pendulum causes a similar jump - maybe motion, maybe air movement, or both. Also, I have the Atlantic ocean crashing 50 meters from the house...Perhaps Fishing would be a more successful pastime? Joe, you are in a unique position to repeat an experiment that has only been done once! You have a pendulum in a location with regular seismic noise which is, uniquely, properly instrumented to measure its motion. Many years ago Doug Bateman noticed that the pendulum of his clock had a tiny motion even when not having been impulsed. This seemed to be due to vibration of the support point. Doug made measurements using a travelling microscope. Philip Woodward analysed the motion of a pendulum subject to random motion of the support with an important conclusion, that the main cause of error was small random changes in amplitude via circular deviation, and the effect of this increases with Q! This is unlike errors caused by internal impulse noise which are reduced by higher Q. Other than Doug's observations, to my knowledge the only other observation has been by Bryan Mumford (of the Microset) who logs the timekeeping of the courthouse clock in Santa Barbara. He saw a large transient in the period caused by an earthquake in California, and based on that a lot of horologists argue that high Q is undesirable, but no one has done proper measurements. So it would be really interesting to just turn off the impulsing, let the pendulum coast down, and log the remaining motion for as long as convenient, if the SNR of your angle sensor permits. No need for very rapid sampling either, the bandwidth of the motion is a fraction of a hertz. |
| 01/09/2023 06:57:27 |
|
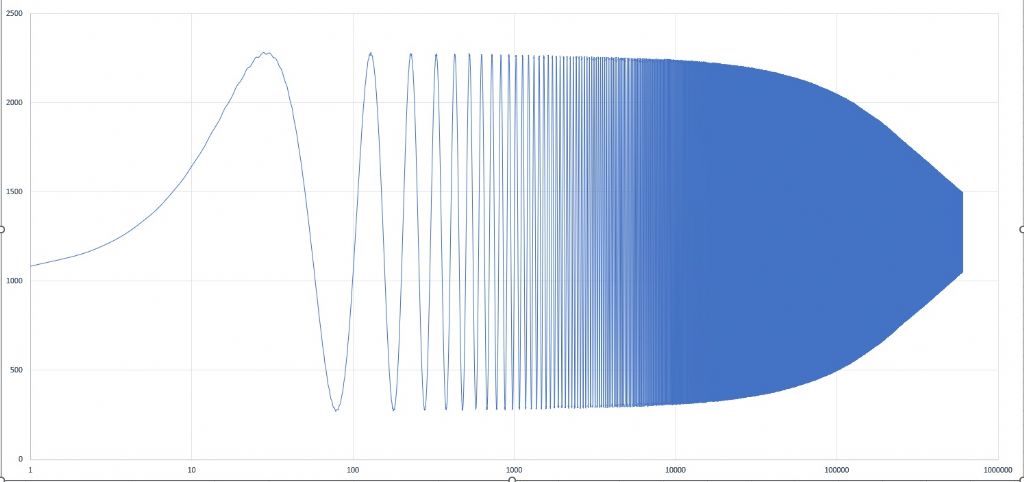
No, I mean log amplitude but linear time. For each cycle take its peak, normalise to the starting amplitude, then take the log. The resulting value for pure exponential decay will be a straight line with negative slope. |
| Thread: Isochronous knife edge suspension? |
| 01/09/2023 06:50:11 |
Obviously the whole thing has to be isochronous. You can compute the effective "length" of a compound pendulum by adding together all the moments of inertia and moments of mass of its components in a spreadsheet. As for the roller radius, Woodward's second paper has the necessary analysis but that would need extending to derive the necessary radius (if indeed there is one). I'll send you a PM. |
| 31/08/2023 17:09:07 |
Have you got copies of Philip Woodward's articles? |
| 31/08/2023 08:58:53 |
Exactly. |
| Thread: A combinatorial problem. |
| 31/08/2023 08:58:09 |
Indeed, see 4th post down. |
| Thread: Isochronous knife edge suspension? |
| 31/08/2023 07:25:50 |
To be clear, there is only one cycloidal path that makes the pendulum isochronous and that's one where the roller radius (or diameter?) equals the pendulum length. Anything else just approximates the cycloid for small angles in a way that can correct the isochronism. Anyway the path of the bob for this setup is epi-trochoidal. As far as I know everyone who has looked at this (mainly Woodward) just assumed that the magnetic version would be impracticable and the calculations of the required roller diameter haven't been done, you're pioneering here Dave! Also one would have to factor in that real pendulums are compound just to make it more interesting. |
| Thread: JoNo's Pendulum |
| 31/08/2023 07:14:37 |
Well, a few points. First Joe, I think your Q is very respectable. Of the same order that a Synchronome has if not having to operate its count wheel. My 'Nome derivative is about 12,000, and Doug Bateman's clock is similar. Looking back through this thread I don't see a mention of your bob mass. Q is defined in the simple model as "w*M/k" where w is angular resonant frequency, M the mass, and k the resistance constant. Your shape will have a lower k but mass is equally important. Nome bobs are usually about 7kg (as is mine being a hefty chunk of CI). They are however blunt cylinders so aerodynamically not so good. If you can increase your bob density (fill it or make it from lead?) that should be a direct was to get higher Q. My tungsten bob is somewhat smaller in mass (5.2kg) but 52mm diameter rather than 80mm, and has chamfered and rounded ends. I think its relatively smaller size and high density is what gives it the higher Q. You plot the decay I think on a linear amplitude scale. It would be interesting to plot it on a log (ln) scale which is more natural for exponential decay. But it's fairly clear that there is a "break point" where the slope decreases. If you are seeing essentially an exponential shape it's a good indication that the loss is primarily aerodynamic - other forms of loss give different shapes. My pendulum test showed exactly such a break point, with a somewhat higher Q for that part of the decay above it. At very low speeds the loss is viscous drag which is proportional to velocity and gives the "ideal" decay shape. As amplitude increases the flow gets more complex and the loss moves towards a square-law with velocity. Douglas Drumheller in the US does a lot of work in this area and you can see some discussion at here. (By the way please feel free to join the HSN forum!) In an HSN article IIRC, Doug links this towards flow vortices detaching from the bob at higher speeds. |
| 29/08/2023 08:54:34 |
Really interesting system Joe. A couple of questions. How do you filter the signal from the synchronous detector? There was a long debate in HSN between Matthys and Bigelow about the significance of any phase shift in the sinusoidal drive oscillator loop. Bigelow used a very simple oscillator circuit where the pendulum was the resonator, using a single op-amp and (zener?) diodes to limit amplitude. The op-amp GBW was 1 MHz, so there was a small excess phase shift at 0.5 Hz which meant that the impulse wasn't quite in phase with the pendulum. Bigelow thought that this was insignificant, Matthys was concerned, I think there's a whole chapter in his book that reflects this debate. I'm also interested in how you achieve the 90* phase shift needed for the pendulum drive, at 0.5Hz! I've wondered about sinusoidal drive for my clock, but not having a proportional angle sensor would probably mean having to phase-lock a digital system and synthesising the sine wave. |
Want the latest issue of Model Engineer or Model Engineers' Workshop? Use our magazine locator links to find your nearest stockist!
Sign up to our newsletter and get a free digital issue.
You can unsubscribe at anytime. View our privacy policy at www.mortons.co.uk/privacy
- *Oct 2023: FORUM MIGRATION TIMELINE*
05/10/2023 07:57:11 - Making ER11 collet chuck
05/10/2023 07:56:24 - What did you do today? 2023
05/10/2023 07:25:01 - Orrery
05/10/2023 06:00:41 - Wera hand-tools
05/10/2023 05:47:07 - New member
05/10/2023 04:40:11 - Problems with external pot on at1 vfd
05/10/2023 00:06:32 - Drain plug
04/10/2023 23:36:17 - digi phase converter for 10 machines.....
04/10/2023 23:13:48 - Winter Storage Of Locomotives
04/10/2023 21:02:11 - More Latest Posts...
- View All Topics
- Reeves** - Rebuilt Royal Scot by Martin Evans
by John Broughton
£300.00 - BRITANNIA 5" GAUGE James Perrier
by Jon Seabright 1
£2,500.00 - Drill Grinder - for restoration
by Nigel Graham 2
£0.00 - WARCO WM18 MILLING MACHINE
by Alex Chudley
£1,200.00 - MYFORD SUPER 7 LATHE
by Alex Chudley
£2,000.00 - More "For Sale" Ads...
- D1-3 backplate
by Michael Horley
Price Not Specified - fixed steady for a Colchester bantam mark1 800
by George Jervis
Price Not Specified - lbsc pansy
by JACK SIDEBOTHAM
Price Not Specified - Pratt Burnerd multifit chuck key.
by Tim Riome
Price Not Specified - BANDSAW BLADE WELDER
by HUGH
Price Not Specified - More "Wanted" Ads...
Do you want to contact the Model Engineer and Model Engineers' Workshop team?
You can contact us by phone, mail or email about the magazines including becoming a contributor, submitting reader's letters or making queries about articles. You can also get in touch about this website, advertising or other general issues.
Click THIS LINK for full contact details.
For subscription issues please see THIS LINK.
Model Engineer Magazine
- Percival Marshall
- M.E. History
- LittleLEC
- M.E. Clock
ME Workshop
- An Adcock
- & Shipley
- Horizontal
- Mill
Subscribe Now
- Great savings
- Delivered to your door
Pre-order your copy!
- Delivered to your doorstep!
- Free UK delivery!









 Register
Register Log-in
Log-in


